Объяснение:
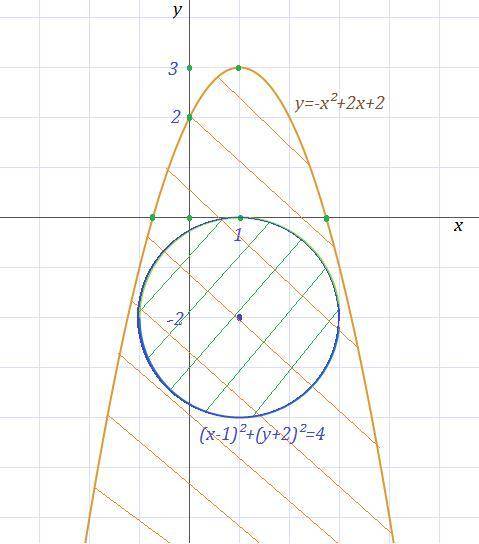
Множество точек, удовлетворяющих неравенству y≤-x²+2x+2 - это часть плоскости ограниченная параболой у= -x²+2x+2 и лежащая внутри этой параболы. Сама парабола у= -x²+2x+2 имеет вершину в точке ( 1,3 ), её ветви направлены вниз .
Множество точек, удовлетворяющих неравенству (x-1)²+(y+2)²≤4 - это часть плоскости, ограниченная окружностью (x-1)²+(y+2)²=4 и находящаяся внутри неё, то есть это круг с центром в точке ( 1, -2) , радиус которого равен R=2 .
Пересечением этих двух множеств являются точки круга вместе с его границей ( окружностью (x-1)²+(y+2)²=4 ) .
На чертеже область заштрихована двумя пересекающимися штриховками.
x^2+2x≤1
x^2+2x-1≤0
x^2+2x-1=0
x1=-2+кор.кв(4+4)/2=(-2+кор.кв.(8))/2≤0
x2=-2-кор.кв(4+4)/2=(-2-кор.кв.(8))/2≤0
(-2+кор.кв.(8))/2примерно=0,414
(-2-кор.кв.(8))/2 примерно =-2,414
Отмечаем точки 0,414 и -2,414 на числовой прямой, выделяем область общую(удовлетворяющую двух корням уравнения)
x (-бесконечности;-2.414]