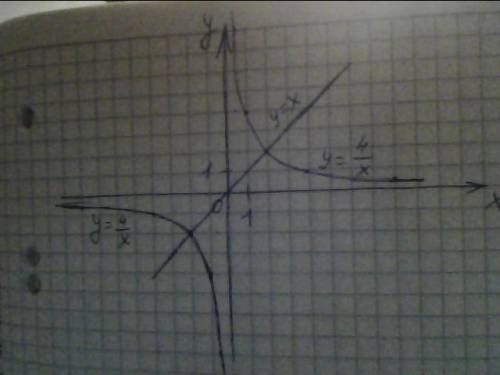
Итак, имеем две функции у= 4/х и у= х
Для каждой из них чертим табличку
у=х прямая, проходящая через точку (0;0), значит нужна еще одна точка, например, (2;2)
у=4/х - гипербола, нужно неск точек как положительных так и отрицательных но не х=0
х= 0,5 1 2 4 8 -0,5 -1 -2 -4 -8
у= 8 4 2 1 0,5 -8 -4 -2 -1 -0,5
Теперь по точкам строим два графика ( график второй функции состоит из двух частей) и смотрим точки пересечения графиков. Эти точки и пишем в ответ.
ответ: (2;2) и (-2;-2)
Смотри вложение.
25^(х^2+0.5) - 5^x^2=5^(x^2+3) - 25
5^(2х^2+1) - 5^x^2=125 * 5^x^2 - 25
5*5^2х^2 - 5^x^2 - 125 * 5^x^2 + 25 =0
5*5^2х^2 - 126 * 5^x^2 + 25 =0
Пусть 5^x^2 = а,тогда
5a^2-126a+25=0
a1=0,2=1/5
a2=25
так как 5^x^2 = а, то
1) при а1=1/5=5^(-1) 5^x^2= 5^(-1), тоесть х^2 = -1 - такого не может быть
2) при а2=25= 5^2 5^x^2= 5^2, тоесть х^2 = 2,
тогда х1= корень(2)
х2= - корень(2)
Надо найти х1+х2= корень(2) + (- корень(2))=0
ответ: 0