А) (х - 7)(х + 3); в) (3а - b)(2a + 5b);
б) (2у + 1)(5у - 6); г) (х - 6)(х² + 2х - 3).
2. Разложить на множители:
a) 2x(a + c) - 5(a + c); в) ab + ac + xb + xc;
б) 3x(m - n) - (n - m); г) 5a + 5b - am - bm.
3. У выражение:
а) -5с²(6 - 4с)(2с² + 7с); б) а(а - 3) + (а + 1)(а + 4)
4. Решить задачу:
Клумба прямоугольной формы окружена дорожкой, ширина которой 1 м. Площадь дорожки
26 м². Найти стороны клумбы, если одна из них на 5 м больше другой.
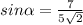следовательно 
( x + 2)²( (x + 2)² - 4) = 5
( x + 2)²( x² + 4x + 4 - 4) = 5
( x + 2)²( x² + 4x) = 5
(x² + 4x)(x² + 4x + 4) = 5
x⁴ + 4x³ + 4x² + 4x³ + 16x² + 16x - 5 = 0
x⁴ + 8x³ + 20x² +16x- 5 =0
Разложим на множители и решим:
(x² + 4x - 1)(x² + 4x + 5) = 0
Произведение равно 0,когда один из множителей равен 0,значит,
x² + 4x - 1 = 0
D = b² - 4ac = 16 - 4×(-1) = 20
x1 = ( - 4 + 2√5) / 2 = - 2(2 - √5)/2 = - (2 - √5) = √5 - 2
x2 = ( - 4 - 2√5)/2 = - 2( 2 + √5) / 2 = - ( 2 + √5) = - √5 - 2
x² + 4x + 5 = 0
D = b² - 4ac = 16 - 4×5 = - 4 - дискриминант отрицательный,значит,корней нет.
ответ: x1 = √5 - 2, x2 = - √5 - 2.