Question

1. Преобразуйте в многочлен стандартного вида:
а) (а3 + 2) (а – 3)
б) (m – 4) ( m + 5)
в) (3х – 1) (2х + 5)
г) – 5х (–х – 2) (2х3 – 3 + 4 х)

2. У выражение: а) (х + 2) (х -5) – 3х (1 – 2х) б) (а + 6) (а – 3) + (а – 4) (а + 5)

3. Решите уравнение: а) 14 х2 – (2х – 3) (7х + 4) = 14 б) (2х + 6) (7 – 4х) = (2 – х) (8х + 1) + 15

4. Решите задачу:
Длина прямоугольника вдвое меньше его ширины.
Если длину уменьшить на 2 дм, а ширину увеличить на 7 дм, то
его площадь увеличится на 19 дм2. Найти длину и ширину
прямоугольника

Answer 1

первое задание, если не надо решать

Answer 2

1.

а) (а³ + 2) (а – 3)  = a⁴ - 3a³ + 2a - 6

б) (m – 4) ( m + 5)  = m² + 5m - 4m - 20 = m²+ m - 20

в) (3х – 1) (2х + 5)  = 6x² + 15x - 2x - 5 = 6x² + 13x - 5

г) – 5х (–х – 2) (2х³ – 3 + 4 х) = (5x² + 10x)(2x³-3+4x) = 10x⁵ - 15x² + 20x³ +20x³ - 30x + 40x² = 10x⁵ + 40x³ + 25x² - 30x

2.

а) (х + 2) (х -5) – 3х (1 – 2х) = x² - 5x + 2x - 10 - 3x + 6x² = 7x² - 6x - 10

б) (а + 6) (а – 3) + (а – 4) (а + 5) = a² - 3a + 6a - 18 + (a² +5a - 4a - 20) =  a² - 3a + 6a - 18 + a² + 5a - 4a - 20 = 2a² + 4a - 38 | :2 = a² +2a - 19

3.

а) 14х² – (2х – 3) (7х + 4) = 14

14x² - (14x² + 8x -21x - 12) = 14

14x²-14x²+13x=14-12

13x = 2

x = 2/13

б) (2х + 6) (7 – 4х) = (2 – х) (8х + 1) + 15

14x - 8x² + 42 - 24x = (16x + 2 -8x² - x) + 15

-8x² - 10x -15x + 8x² = 15 + 2 - 42

-25x = -25

x = 1

4.

Пусть x - длина прямоугольника, тогда 2x - ширина

$\left \{ {{x*2x=S} \atop {(x-2)(2x+7) = S - 19}} \right.$  ⇒ $\left \{ {{2x^{2} = S } \atop {2x^{2} +7x - 4x - 14 = 2x^{2} - 19 }} \right.$

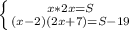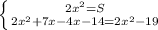
2x² + 7x - 4x - 14 = 2x² + 19

3x =  19 + 14

3x = 33

x = 11 - длина прямоугольника

11 * 2 = 22 - ширина прямоугольника