5 монет -всего
2 монеты- по 2 рубля
2/5= 0,4
Объяснение:
1) Неравенства старайтесь привести к такому виду, чтобы справа был 0, а слева произведение скобок.
Дальше находите нули в каждой скобке отдельно и решаете по методу интервалов.
2) Для области определения (ОДЗ) есть несколько ограничений:
А) Знаменатель дроби не должен быть равен 0.
Б) Число под корнем чётной степени (квадратным, 4, 6 и т.д степени) должно быть >= 0.
Заметьте, что для корней нечётных степеней (кубического, 5, 7 и т.д) такого ограничения нет.
В) Основание логарифма должно быть > 0 и не равно 1.
Число под логарифмом должно быть > 0.
Г) Число под тангенсом не должно быть равно Π/2 + Πk, где k - целое.
Число под котангенсом не должно быть равно Πk, где k - целое.
Вот и всё.
Составляете соответствующие неравенства и решаете их.
После того, как нашли область определения, не забудьте вернуться к решению самого уравнения!
1. Преобразуйте уравнение (х + 7)2 - 4х = 2х(х - 5) к виду ax2 + bx + c = 0. Укажите старший коэффициент, второй коэффициент и свободный член этого уравнения.
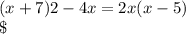
Переобразуем:
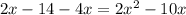
Переносим в общую сторону (левую) и меняем знаки:
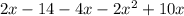
Сокрашаем:
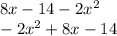
ответ: 
Старший коэффициент: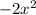 
Второй коэффициент: 8x
Свободный член: -14
2. а) Определите, какое из уравнений является неприведенным квадратным уравнением и найдите его корни:
А) 
В)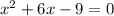 
С)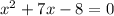 
D)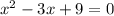 
У неприведенных квадратных уравнениях, старшие коэффициенты не равны 1. (0/5, 3, 5, -17, тд - все неприведенные квадратные уравнения).
A)
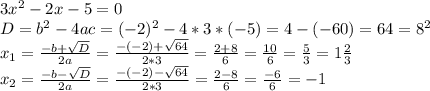
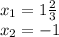
2. б) Составьте приведенное квадратное уравнение, имеющие корни х1= 8, х2 = –2.
По теореме Виета:
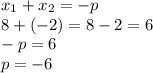
ответ:
3. Дано квадратное уравнение 2х^2 - 16х + с = 0.
а) Определите, при каких значениях параметра с уравнение имеет два одинаковых корня.
Если дискриминант (D) квадратного уравнения равен 0, то уравнение имеет 1 корень, или говорят 
и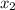 
совпадают.
Если p = 0, то 
ответ: c = 32
3. б) Найдите эти корни уравнения
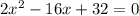
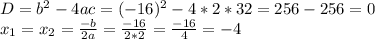
ответ: 
2/5 = 0.4 ответ : 0,4
Думаю это правильный ответ ))