sin (5πx/9) = sin (πx/9) + sin (2πx/9)
sin (5πx/9) - sin (πx/9) = sin (2πx/9)
По формуле разности синусов:
2sin(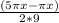
)cos(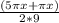
) - sin (2πx/9) = 0;
2 sin(2πx/9)cos(πx/3) - sin(2πx/9)=0;
sin (2πx/9) (2cos(πx/3)-1)=0;
sin (2πx/9)=0 или 2cos (πx/3)=1; cos (πx/3)=1/2
2πx/9=πn, n∈Z или πx/3=π/3+2πn, n∈Z или πx/3=-π/3+2πn, n∈Z;
Сокращаем на π:
2x/9=n, n∈Z или x/3=1/3+2n, n∈Z или x/3=-1/3+2n, n∈Z;
x=9n/2 или x=6n+1 или x=6n-1
Теперь отбираем корни уравнения, принадлежащие промежутку (4;8)
4<(9/2)n<8; 8/9<n<16/9; n=1, x=4,5
4<6n+1<8; 3<6n<7; 1/2<n<7/6; n=1; x=6+1=7;
4<6n-1<8; 5<6n<9; 5/6<n<3/2; n=1; x=6-1=5
ответ: x={4,5;5;7}
Введем обозначения:Х-количество ступенек неподвижного эскалатора.
Т-время прохода "быстрого" Х ступенек.
Х/Т-скорость "быстрого"
Х/2Т-скорость "медленного"
60*Т/X-время быстрого по движущемуся эскалатору
40*2Т/X-время медленного по движущемуся эскал.
Х-60 и Х-40 количество непройденных ступенек быстрым и медленным.
Теперь находим скорость эскалатора через количество непройденных ступенек быстрого и медленного за соответствующее время:
(Х-60)/(60Т/Х)=(Х-40)/(40*2Т/Х)
(Х-60)/60=(Х-40)/40*2, X=120ступенек.