В решении.
Объяснение:
1)
а)√72 = √36*2 = 6√2;
б)0,01*√800 = 0,01*√100*8 = 0,01*10√8 = 0,1√8;
в)√28 = √4*7 = 2√7;
г)0,2√75 = 0,2*√25*3 = 0,2*5√3 = √3;
д)√98 = √49*2 = 7√2;
е)0,02*√1200 = 0,02*√400*3 = 0,02*20√3 = 0,4√3;
ж)1/5*√50 = 0,2*√25*2 = 0,2*5√2 = √2;
з)√27 = √9*3 = 3√3.
2)
а)3√5а = √9*5а = √45а;
б)-10√0,2b = -√100*0,2b = -√20b;
в)5√2а = √25*2а = √50а;
г)-20√0,1b = -√400*0,1b = -√40b;
д)4√5 = √16*5 = √80;
е)-3√а = -√9а;
ж)9√2 = √81*2 = √162;
з)2√b = √4b.
3)
а) √27 и 4√3
√27 = √9*3 = 3√3
√27 < 4√3;
б)√18 и 4√2
√18 = √9*2 = 3√2
√18 < 4√2
в)3√2 и 2√3
3√2 = √9*2 = √18; 2√3 = √4*3 = √12
3√2 > 2√3;
г)5√3 и 3√5
5√3 = √25*3 = √75; 3√5 = √9*5 = √45
5√3 > 3√5.
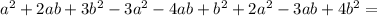

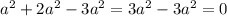
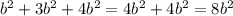
 - Тут вынес знак минуса за скобку, чтобы было понятно, что разность -4ab-3ab дает сумму с отрицательным знаком.
- Тут вынес знак минуса за скобку, чтобы было понятно, что разность -4ab-3ab дает сумму с отрицательным знаком.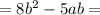
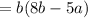
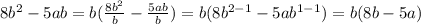

 "
"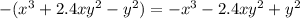

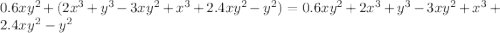

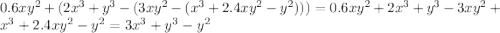
Для нахождение наименьшего и наибольшего значения на отрезке найдем значение функции в критической точке и на концах отрезка - при x = 0, x = 3 и x = 6.
Первая точка в заданный промежуток не попадает, а вторая совпадает с левым ее концом, поэтому для нахождение наименьшего и наибольшего значения на отрезке достаточно найти значение функции на концах отрезка: при х = 1 и х = 3.
Для нахождение наименьшего и наибольшего значения на отрезке найдем значение функции в критических точках и на концах отрезка - при x = -4, x = -1, x = 3 и х = 4: