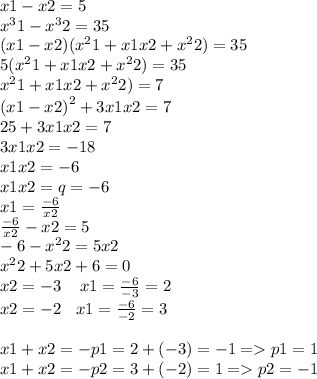
Ремарка:
в большинстве случаев использовалась расширенная теорема Виета, которая есть не что иное как счелканье уравнений как семечек в уме. Я рекомендую вам изучить очень хорошо метод переброски, который, поверьте моему опыту, упросить вам жизнь.
Объяснение:
1)

2)
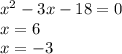
3)
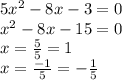
4)
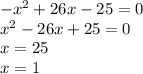
5)
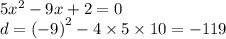
То есть уравнение корней не имеет, так как дискриминант отрицательный.
6)
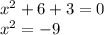
Уравнение корней не имеет, так как какое бы мы число к квадрату не поднесли, результат всегда будет положительный, а не отрицательный, как вот (-9).
7)
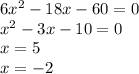
8)
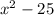
Если задача стоит разложить на множители, то имеем:
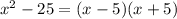
Если задача стоит найти корни уравнения, то имеем:
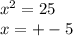
9)
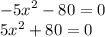
Уравнение не имеет корней, так как левая часть всегда > 0, а не равна ему. Действительно, какое бы мы число не подставили вместо x, оно всегда будет ≥ 80.
10)
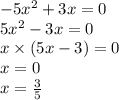
11)
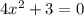
Уравнение не имеет корней, аналогичная ситуация как в уравнении 9.
12)
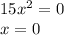
1)
{x1-x2 = 5
{x1³-x2³ = 35
{x1-x2 = 5
{(x1-x2)(x1²+x1•x2+x2²) = 35
{x1 = 5+x2
{x1²+x1•x2+x2² = 7
(5+x2)²+x2(5+x2)+x2²-7 = 0
25+10x2+x2²+5x2+x2²+x2²-7 = 0
3x2²+15x2+18 = 0
x2²+5x2+6 = 0
По Виету:
[x2 = -2
[x2 = -3
[x1 = 5+x2 = 3
[x1 = 5+x2 = 2
(3; -2), (2; -3)
2)По виету
{x1+x2 = -p =3-2 = 1
{x1•x2 = q = -6
x²-x-6 = 0
3)По Виету:
{-p = x1+x2 = 2-3 = -1
{x1•x2 = q = -6
x²+x-6 = 0