Для решения этой задачи используем формулы арифметической прогрессии.
а₁=5 [в первый день 5 капель]
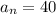[день, в который нужно выпить 40 капель]
d=5 [разность арифметической прогрессии, т.к. каждый день дозировка увеличивается на одну и ту же величину - 5 капель]
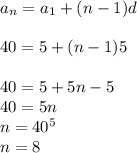
На восьмой день дозировка составит 40 капель.
По формуле суммы n первых членов арифметической прогрессии найдм сколько всего капель нужно выпить больному за 8 дней.
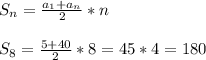
180 капель должен выпить больной за первые 8 дней лечения.
В последний период лечения больной должен уменьшать дозировку каждый день на 5 капель, и с дозировки в 40 капель дойти до 5 капель.
На это ему понадобиться 8 дней (также, как и в первый период лечения).
Суммарное количество капель, которые должен выпить больной за эти 8 дней, составит 180.
В середине лечения больной должен три дня подряд пить по 40 капель. Два раза по 40 капель мы уже учли. Поэтому к общей сумме добавим только 40.
180+180+40 = 400 (капель) - должен выпить больной за весь период лечения.
В одном пузырьке содержится 200 капель лекарства. Значит больному нужно купить 400:200 = 2 пузырька лекарства.
ответ: 2 пузырька.
ax² + bx + c = 0 - квадратное уравнение (a ≠ 0), называется неполным, если b = 0, или c = 0, или оба сразу (b = 0 и c = 0). Разберем все эти случаи.
1) b = 0 и c ≠ 0
ax² + c = 0
ax² = -c
x² = -c / a
x² ≥ 0, поэтому для того, чтобы уравнение не имело корней достаточно -c / a < 0; c / a > 0 - получили ответ на первый вопрос
2) b ≠ 0; c = 0
ax² + bx = 0
x·(ax + b) = 0
x₁ = 0; x₂ = -b / a
То есть корни будут всегда, и мы получили ответ на второй вопрос задачи:
(при b ≠ 0; c = 0; Уравнение ax² + bx = 0 имеет 2 корня, один из которых 0)
3) b = 0 и c = 0
ax² = 0
x = 0, то есть всегда корнем будет 0
Объяснение:
эта су ка пенивайз,че за пасть,она ест моих детей