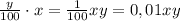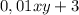.
, что составляет 90% серебра от веса всего сплава, так как по условию задачи мы получим сплав 900 пробы ( 900 проба серебра значит, что сплав содержит 900 г серебра на 1000 г от всего веса, то есть 90%). То есть с другой стороны серебра во 2 сплаве будет 
.
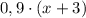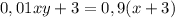
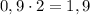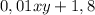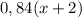кг .
.
кг .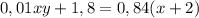
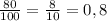частям серебра в трёхгилограммовом сплаве .
(4; -1)
Объяснение:
Так как левые части уравнений равны, можем приравнять и правые части, получим:
(х - 6)/(x - 2) = (x - 8)/x, теперь избавимся от дробного выражения, общий знаменатель х(х - 2), надписываем над числителями дополнительные множители, получаем:
х * (х - 6) = (x - 2) * (x - 8), раскрываем скобки:
х² - 6х = х² - 2х - 8х + 16
х² - х² -6х + 10х = 16
4х = 16
х = 4, теперь значение х подставим в любое уравнение, получим у:
у = (4 - 6)/(4 - 2) = -2 / 2 = -1
у = (4 - 8)/4 = -4 / 4 = -1