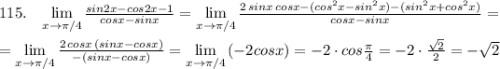
![98.\; \; \; \lim\limits _{x \to 0}\frac{cos2x-1}{x^2}=\Big[\; 1-cos\alpha =2sin^2\frac{\alpha }{2}\; \Big]=\lim\limits _{x \to 0}\frac{-2sin^2x}{x^2}=\\\\=\Big[\; sinx\sim x\; ,\; esli\; x\to 0\; ;\; \; sin^2x=(sinx)^2\sim x^2\; \Big]=\lim\limits _{x \to 0}\frac{-2\cdot x^2}{x^2}=-2](/tpl/images/1077/8104/124bc.png)
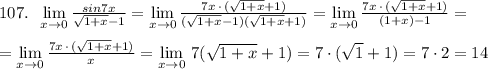
![112.\; \; \lim\limits _{x \to \pi /2}\Big(x-\frac{\pi}{2}\Big)\cdodt tgx=\Big[\; t=x-\frac{\pi}{2}\; ,\; t\to 0\; \Big]=\lim\limits _{t \to 0}\; (\, t\cdot tg(t+\frac{\pi}{2})\, )=\\\\=\lim\limits _{t \to 0}\; \frac{t\cdot sin(t+\frac{\pi}{2})}{cos(t+\frac{\pi}{2})}=\lim\limits _{t \to 0}\; \frac{t\cdot sin(t+\frac{\pi}{2})}{-sint}=\lim\limits _{t \to 0}\; \frac{t\cdot sin(t+\frac{\pi}{2})}{-t}=\lim\limits _{t \to 0}\; (-sin\frac{\pi}{2})=-1](/tpl/images/1077/8104/0dd6a.png)
![113.\; \; \lim\limits _{x \to \pi /6}\frac{1-2sinx}{\frac{\pi}{6}-x}=\lim\limits _{x \to \pi /6}\frac{2\, (\frac{1}{2}-sinx)}{\frac{\pi }{6} -x}=2\lim\limits _{x \to \po /6}\frac{sin\frac{\pi}{6}-sinx}{\frac{\pi}{6}-x}=\\\\=2\lim\limits _{x \to \pi /6}\frac{2\, sin(\frac{\pi}{12}-\frac{x}{2})\cdot cos(\frac{\pi}{12}+\frac{x}{2})}{\frac{\pi}{6}-x}=\Big[\; sina\sim a,\; a\to 0\; \Big]=4\lim\limits _{x \to \pi /6}\frac{(\frac{\pi}{12}-\frac{x}{2})\cdot cos(\frac{\pi}{12}+\frac{x}{2})}{\frac{\pi -6x}{6}}=](/tpl/images/1077/8104/9bf49.png)
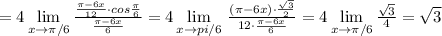
опишу в общем виде: составляешь таблицу со строками «туда» и «обратно». Там расстояние (S) будет одинаковое, скорость (v) «туда» обозначим за х, а скорость «обратно» за х+2. Время «t» выражаем через формулы скорости v=S/t, НО! Во времени «обратно» ещё добавляем два отдельно от дроби. Дальше составляем уравнение и домножаем каждую дробь и двойку на х(х+2), то есть приводим к общему знаменателю-единице. Раскрываем скобки, сокращаем, получившее квадратное уравнение -2х^2-4х+448=0 делим на -2 и получаем х^2+2х-224=0. Через дискриминант (равный 900) решаем уравнение, получаем корни 14 и -16. -16 не подходит, потому что скорость не может быть отрицательной. Прибавляем к 14 два (по условию) и получаем 16. Вторую хз как решать

2. 10
3. В первом - 15, во втором - 45, в двух - 60.
4. Верно при любом значении x.
5. 44
Объяснение:
2.
Вся дорога - 26 мин.
Идет пешком - на 6 мин. дольше, чем едет на автобусе
Едет на автобусе - ? мин.
Пусть x - время, которое Таня едет на автобусе, тогда x + 6 - время, которое Таня идет пешком.
Составим уравнение:
x + 6 + x = 26
2x + 6 = 26
2x = 26 - 6
2x = 20
x = 10
ответ: Таня едет на автобусе 10 минут.
3.
1 сарай - в 3 раза больше сена, чем во 2.
2 сарай - ? тонн сена.
После того, как из первого сарая увезли 20 тонн сена, а во второй привезли 10 тонн сена, в обоих сараях сена стала поровну.
Сколько тонн сена было в двух сараях первоначально?
Пусть во втором сарае было x тонн сена, тогда в первом сарае было 3x тонн сена. Зная, что после того, как из первого сарая увезли 20 тонн, а в первый привезли 10 тонн, количество сена в сараях уровнялось, мы можем составить уравнение:
1) 3x - 20 = x + 10
3x - x = 10 + 20
2x = 30
x = 15 (тонн сена) - было во втором сарае
2) 3 * 15 = 45 (тонн сена) - было в первом сарае.
3) 15 + 45 = 60 (тонн сена)
ответ: первоначально в первом сарае было 45 тонн сена, во втором - 15 тонн сена, а в двух сараях - 60 тонн сена.
4.
7x - (x + 3) = 3(2x - 1)
7x - x - 3 = 6x - 3
7x - x = 6x
6x = 6x
Будет верно при любом значении x.
5.
Масса ящика с яблоками = 22кг + 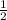 его массы.
его массы.
Масса ящика с яблоками - ?
Пусть x - масса ящика с яблоками, тогда x : 2 - половина массы.
Составим уравнение:
x = 22 + x : 2
x = 22 + 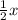
2x = 44 + x
2x - x = 44
x = 44
ответ: масса ящика с яблоками - 44 кг.