1) 2ax³ - 16ay³ = 2a(x³ - 8y³) = 2a(x³ - (2y)³) = 2a(x - 2y)(x² + 2xy + 4y²)
2) y² - 10y + 25 - 3xy + 15x = (y² - 10y + 5²) - 3x(y - 5) = (y - 5)² - 3x(y - 5) = (y - 5)(y - 3x - 5)
3) x² + 2xy + y² + 2x + 2y + 1 = (x² + 2xy + y²) + (2x + 2y) + 1 = (x + y)² + 2(x + y) + 1 = (x + y + 1)²
Длина поезда 600 метров.
Объяснение:
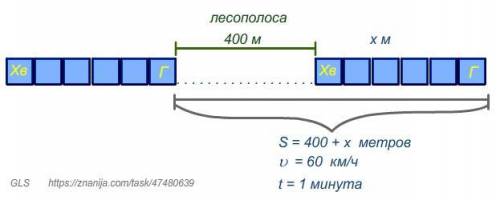
Решим задачу: поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо лесополосы, длина которой 400 м, за одну минуту. Найди длину поезда в метрах.
1) Для начала нужно понять, что значит поезд проезжает мимо лесополосы за одну минуту.
Ориентироваться будем по голове поезда - первому вагону.
Когда первый вагон поравнялся с началом лесополосы, начался отсчет времени движения поезда вдоль лесополосы.
А закончился отсчет времени, когда поравнялись конец лесополосы и конец последнего вагона - хвоста поезда 1 минута.
За это время голова поезда проехала всю лесополосу и еще проехала такое расстояние, чтобы хвост поезда сравнялся с концом лесополосы, то есть голова вперед на длину поезда.
Значит за 1 минуту поезд расстояние, равное длине лесополосы плюс длина поезда.
2) Пусть длина поезда равна x метров. Путь, пройденный поездом равен 400 + x метров.
3) Скорость поезда 60 км/ч, это значит поезд за 1 час (= 60 минут расстояние 60 км, а за 1 минуту он проходит расстояние 1 км.
1 км = 1000 м.
4) За 1 минуту поезд 1000 м, это расстояние равно сумме длины лесополосы и длины поезда.
400 + x = 1000; x = 1000 - 400 = 600 (м).
Длина поезда 600 метров.
2x² + 7x - 4 = 0
Это квадратное уравнение решения много, самый частый -- через дискриминант (D).
Квадратное уравнение в общем виде выглядит так:
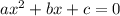
где a, b, c -- коэффициенты, a ≠ 0
Формула дискриминанта:
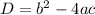
Формула корней:
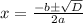
При этом от дискриминанта зависит количество корней в уравнении:
Если D > 0, то уравнение имеет 2 корня
Если D = 0, то уравнение имеет 1 корень
Если D < 0, то уравнение не имеет корней
Теперь решение:
2x² + 7x - 4 = 0
В нём a = 2, b = 7, c = -4. Подставим эти значения в формулу дискриминанта:
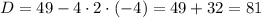
D > 0, значит уравнение имеет 2 корня.
Найдём корень из дискриминанта и корни уравнения:
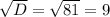
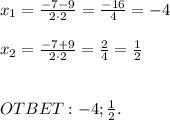
1) 2a(x³-8y³)= 2a(x-2y)(x²+2xy+4y²)
2) (y-5)²-3x(y-5)= (y-5)(y-5-3x)
3) (x+y)²+2(x+y)+1= (x+y+1)²= (x+y+1)(x+y+1)