Решение.
Обозначим стороны прямоугольника как x и y.
Тогда периметр прямоугольника равен:
2(x+y)=26
Сумма площадей квадратов построенных на каждой из его сторон (квадратов, соответственно, два и это квадраты ширины и высоты, поскольку стороны смежные) будет равна
x2+y2=89
Решаем полученную систему уравнений. Из первого уравнения выводим, что
x+y=13
y=13-y
Теперь выполняем подстановку во второе уравнение, заменяя x его эквивалентом.
(13-y)2+y2=89
169-26y+y2+y2-89=0
2y2-26y+80=0
Решаем полученное квадратное уравнение.
D=676-640=36
x1=5
x2=8
Теперь примем во внимание, что исходя из того, что x+y=13 (см. выше) при x=5, то y=8 и наоборот, если x=8, то y=5
ответ: 5 и 8 см
Воспользуемся методом вс угла.
Рассмотрим уравнение вида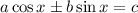 , где
, где 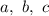 — коэффициенты,
— коэффициенты, 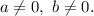
Разделим обе части этого уравнения на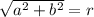
Получим:
Коэффициенты уравнения обладают свойствами синуса и косинуса, а именно: модуль каждого из них не превосходит единицы, а сумма их квадратов равна 1.
Тогда можно обозначить их соответственно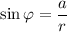 и
и 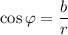 (здесь
(здесь 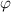 — вс угол) и уравнение примет вид:
— вс угол) и уравнение примет вид:
Из формулы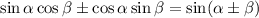 имеем:
имеем:
Решим уравнения:
Воспользуемся формулой косинуса суммы / разности:
Имеем:
ответ: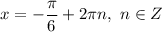
Воспользуемся формулой синуса суммы / разности:
Имеем:
ответ: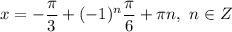
Примечание. Выбор формулы сложения для синуса или косинуса не является принципиальным. Здесь для удобства выбраны формулы именно такие, чтобы под тригонометрической функцией стоял аргумент со знаком плюс. Можно непосредственно пользоваться формулой для решения такого рода уравнений.
Второй метод: универсальная тригонометрическая подстановка.
Для уравнений вида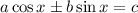 , где
, где 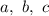 — коэффициенты,
— коэффициенты, 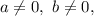 воспользуемся выражениями тригонометрических функций через тангенс половинного аргумента:
воспользуемся выражениями тригонометрических функций через тангенс половинного аргумента:
Перепишем уравнение:
Сделаем соответствующую замену: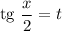
Получили уравнение:
После решения данного уравнения (обычно, их 2) следует вернутся к замене и получить решения:
Для заданных уравнений более рациональным является первый метод решения, потому что их не сложно свести к уравнению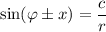 , а процедура выискивания корней дробно-рационального уравнения для второго метода — это еще один относительно большой шаг для решения такого рода уравнений.
, а процедура выискивания корней дробно-рационального уравнения для второго метода — это еще один относительно большой шаг для решения такого рода уравнений.