В иррациональных уравнениях кроме ОДЗ нужно всегда учитывать дополнительные условия (ДУ) или всегда для проверки подставлять полученные корни в исходное уравнение.
Рассмотрим исходное уравнение: 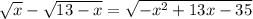
Далее мы возводим это уравнение в квадрат, но это неэквивалентный переход - например, неправильное равенство -1 = 1 переходит в правильное 1 = 1, поэтому на этом этапе легко приобрести лишние корни, что и произошло.
В правой части исходного уравнения находится неотрицательный корень, поэтому в ДУ необходимо потребовать неотрицательность левой части: 
Как раз это ДУ и позволяет в процессе решения откинуть лишний корень 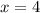
Пусть х км в час - скорость первого, у км в час - скорость второго.
1 мин = (1/60) часа
За 1 мин первый проехал (х/60) км,
второй (y/60) км
Первый проехал на 146 м =0,146 км больше, поэтому
(x/60)- (y/60)=0,146 ⇒ x-y=0,146*60 ⇒ y=x-8,76
Путь пройденный первым за 1 минуту равен (1/120) всей трассы
x/60 =S/120 ⇒ S=2x
Первый проехал дистанцию 2х км со скоростью х км в час
за (S/x)=(2x/x)=2 часа.
и финишировал на 30 мин раньше, чем второй.
Значит второй проехал (2x-0,146) км за 2,5 часа со скоростью
y=x-8,76
Уравнение:
(2x-0,146) =2,5*(х-8,76)
2х-0,146=2,5х-21,9
0,5х=21,9-0,146
х=43,508 км в час
Объяснение:
1)Если две прямые параллельны, то при пересечении их с третьей секущей накрест лежащие углы равны.
При пересечении двух параллельных прямых третьей прямой, образованные ими соответственные углы равны
При пересечении двух параллельных прямых третьей прямой, сумма образованных ими внутренних односторонних углов равна 180°
2). Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.
3)Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним
ΔАВС, ∠А=46°, внешний угол при вершине С равен 107°.
∠В=107°-46°=61°