АВСД - равнобокая трапеция, АВ=СД, ВС=6 см, ∠АВС=120° , ∠САД=30°. Найти АС.
Так как ∠АВС=120°, то ∠ВАД=180°-120°=60° ,
∠САД=30° ⇒ ∠ВАС=∠ВАД-∠САД=60°-30°=30° .
Значит диагональ АС - биссектриса ∠А .
∠АСВ=∠САД=30° как внутренние накрест лежащие при АД || ВC и секущей АС ⇒ ΔАВС - равнобедренный , т.к. ∠ВАС=∠АСВ .
Значит, АВ=АС=6 см .
Опустим перпендикуляры на основание АД из вершин В и С: ВН⊥АС , СМ⊥АД , получим прямоугольник ВСМН и два треугольника АВН и СМД .
Рассмотрим ΔАВН: ∠ВНА=90°, ∠ВАН=∠ВАД=60° , АВ=6 см ⇒
∠АВН=90°-80°=30°
Против угла в 30° лежит катет, равный половине гипотенузы ⇒ АН=6:2=3 см.
Так как ΔАВН=ΔСМД (по гипотенузе АВ=СД и острому углу ∠ВАД=∠АДС), то МД=АН=3 см.
НМ=ВС=6 см как противоположные стороны прямоугольника ВСМН.
АД=АН+НМ+МД=3+6+3=12 см.



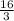
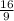
 или х₂ = 1
или х₂ = 1
-1 и -4
Объяснение:
x²+5x+4=0 - квадратное уравнение.
ax²+bx+c=0 - общий вид квадратного уравнения.
В нашем случае, а=1, b=5, c=4
Нам надо найти корни этого уравнения.
Корни ищем по схеме:
1) Вычисляем дискриминант по формуле D=b²-4ac
D= 5²- 4*1*4 = 25 - 16 = 9
2) Находим корни по формуле:
x₁ = (-b+√D)/2a
x₂ = (-b-√D)/2a
x₁ = (-5+√9)/2*1 = (-5+3)/2 = -2/2 = -1
x₂ = (-5-√9)/2*1 = (-5-3)/2 = -8/2 = -4
Итак, корни уравнения найдены. Это числа -1 и -4.
Если вы уже проходили эту тему, то корни можно найти и по теореме Виета, т.к. наше уравнение является приведённым, т.к. квадратным уравнением, у которого а=1. Тогда корни можно найти из соотношений
x₁*x₂=c и x₁+x₂= -b
В нашем случае, x₁*x₂=4 и x₁+x₂= -5
Подбором легко найти корни -4 и -1 (их произведение равно 4, а сумма равна -5)