

Задание 1
1. х² + 15х + 56 = 0
х₁ + х₂ = -15
х₁ · х₂ = 56
х₁ = -7
х₂ = -8
2. х² - 11х + 28 = 0
х₁ + х₂ = 11
х₁ · х₂ = 28
х₁ = 4
х₂ = 7
3. х² - 2х - 35 = 0
х₁ + х₂ = 2
х₁ · х₂ = -35
х₁ = 7
х₂ = -5
4. х² + 3х - 54 = 0
х₁ + х₂ = -3
х₁ · х₂ = -54
х₁ = 6
х₂ = -9
Задание 2
х₁ + х₂ = 3 + (-9) = 3 - 9 = -6
х₁ · х₂ = 3 · (-9) = -27
Наше уравнение:
х² + 6х - 27 = 0
1. Обратно пропорциональная зависимость :
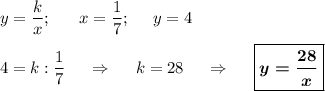
2. Решите графически 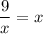
График функции 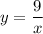 - гипербола в первой и третьей четвертях (k=9>0). Точки для построения :
- гипербола в первой и третьей четвертях (k=9>0). Точки для построения :
x -9 -4,5 -3 -2 -1 1 2 3 4,5 9
y -1 -2 -3 -4,5 -9 9 4,5 3 2 1
График функции y = x - прямая линия, проходящая через начало координат. Точки для построения
x 0 2
y 0 2
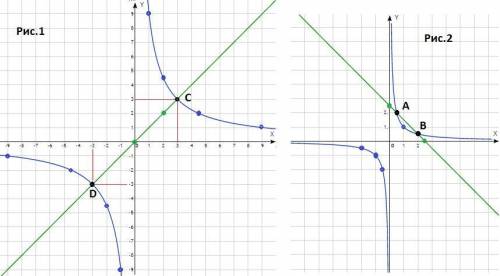
ответ : (-3; -3) и (3; 3) - рис. 1.
3. Графически, сколько решений имеет уравнение 
График функции 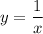 - гипербола в первой и третьей четвертях (k=1>0). Точки для построения :
- гипербола в первой и третьей четвертях (k=1>0). Точки для построения :
x -2 -1 -0,5 0,5 1 2
y -0,5 -1 -2 2 1 0,5
График функции y = 2,5 - x - прямая линия. Точки для построения
x 0 2,5
y 2,5 0
ответ : уравнение имеет 2 решения - рис. 2.
1. Обратно пропорциональная зависимость :
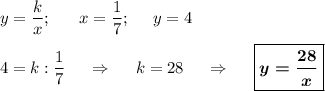
2. Решите графически 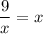
График функции 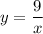 - гипербола в первой и третьей четвертях (k=9>0). Точки для построения :
- гипербола в первой и третьей четвертях (k=9>0). Точки для построения :
x -9 -4,5 -3 -2 -1 1 2 3 4,5 9
y -1 -2 -3 -4,5 -9 9 4,5 3 2 1
График функции y = x - прямая линия, проходящая через начало координат. Точки для построения
x 0 2
y 0 2
ответ : (-3; -3) и (3; 3) - рис. 1.
3. Графически, сколько решений имеет уравнение 
График функции 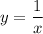 - гипербола в первой и третьей четвертях (k=1>0). Точки для построения :
- гипербола в первой и третьей четвертях (k=1>0). Точки для построения :
x -2 -1 -0,5 0,5 1 2
y -0,5 -1 -2 2 1 0,5
График функции y = 2,5 - x - прямая линия. Точки для построения
x 0 2,5
y 2,5 0
ответ : уравнение имеет 2 решения - рис. 2.
