ответ: x1=3 ; x2=2
Объяснение:
Пусть : x^2-5x+17=n n-натуральное число.
4 коэффициент в разложении бинома :
C (3,n) = n!/(3!*(n-3)!)
Составим уравнение :
n!/(3!*(n-3)!) = 15*n
k!= 1*2*3*4...*k k - натуральное число.
3!=6
n! /(n-3)! = 90*n
n>=3
(n-2)*(n-1)*n = 90*n
n=0 нас не интересует.
(n-2)*(n-1) = 90
n^2-3n -88 = 0
По теореме Виета :
n1= 11 - подходит
n2=-8 - не подходит
x^2-5x+17 = 11
x^2-5x+6=0
По теореме Виета :
x1=3
x2=2

![sin [ 4 arccos ( - \frac{1}{2}) - 2 arcctg \frac{ \sqrt{3} }{3} ] = \\ sin [4* \frac{2 \pi }{3} - 2* \frac{ \pi }{3} ] = \\ sin[ \frac{8 \pi }{3} - \frac{2 \pi }{3} ] = sin(2 \pi ) = 0](/tpl/images/0841/6514/75bd3.png)
 , n,m∈Z
, n,m∈Z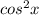 не является корнем ( на ноль делить нельзя), а потом все уравнение почленно разделить на
не является корнем ( на ноль делить нельзя), а потом все уравнение почленно разделить на 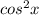
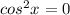
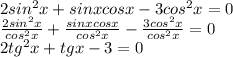
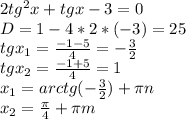
При каком значении x коэффициент 4-го члена в разложении бинома Ньютона (a+b)ⁿ 15 раз больше степени n= x² - 5x +17 .
ответ: 2 или 3
Объяснение:
Коэффициент 4-го члена в разложении бинома Ньютона:
Сn³ = n(n-1)(n-2)/(1*2*3) и по условию равен 15*n, где
n = x² - 5x +17 ∈ ℕ .
n(n-1)*n-2) / (1*2*3) = 15n ⇔ (n-1)*n-2) = 90 ⇔n² -3n +2 =90 ⇔
n² -3n - 88=0 ⇔ || n² - (-8+11)n +(- 8*11)=0 ||
D=3² -4*(-88) =9+352=361=19²
n =(3÷19)/2 ⇒n₁ = - 8_посторонний корень ; n₂=11 .
x² - 5x +17 =11 ⇔ x² - 5x +6 =0 ⇒ x₁ =2 ; x₂ =3.