Объяснение:
1). ma+mb+4a+4b=m×(a+b)+4(a+b)=(a+b)×(m+4)
2). 3x+cy+cx+3y=x×(3+c)+y(c+3)=(3+c)(x+y)
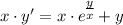
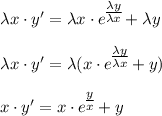
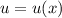с замены:
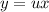, тогда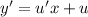 
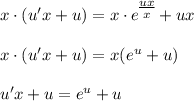
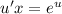
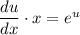- уравнение с разделяющимися переменными.
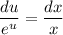- уравнение с разделёнными переменными.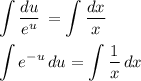
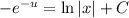- общий интеграл новой функции.
из решения уравнения с разделяющимися переменными, чтобы записать решение исходного однородного уравнения, остаётся выполнить обратную замену: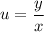 
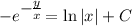- общий интеграл исходного уравнения.
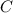. Подставим в общий интеграл начальное условие: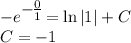
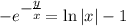- частный интеграл, также является решением данного дифференциального уравнения.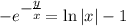
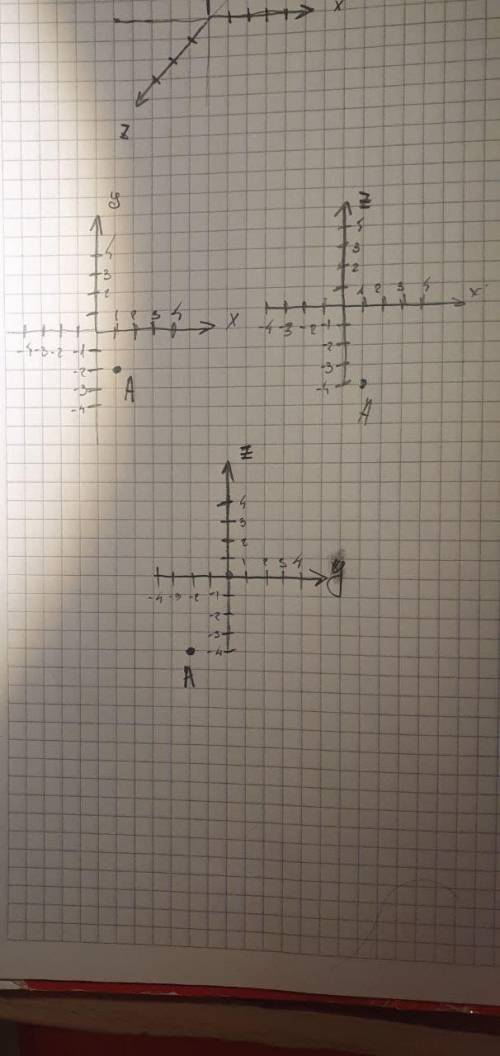
Расстояния:
от точки A до координатной плоскости
1) xy = 4
2) xz = 2
3) yz = 1
Объяснение:
Для начала изображение. Очень сложно изобразить точку в трехмерном пространстве на бумаге, поэтому я нарисовал точку на 3-х плоскостях (xy, xz, yz)
Теперь найдем растояние точки от каждой плоскости. Пусть надо найти расстояние от точки A до плоскости xy. То есть x и y у нас те же а z=0.
Что это значит?
Вспомним формулу расстояния точки А(x1, y1, z1) до точки B (x2, y2, z2)
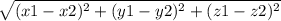
в нашем примере получается что x1 = x2 и y1 = y2. А что получается когда у нас 2 числа при отнимании равны? 0! А z2 у нас 0. Как я объяснял еще раньше.
поэтому функция иммет вид
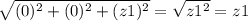
ответ:am+mb+4a+4b=m(a+b)+4(a+b)=(a+b)(m+4)
3x+cy+cx+3y=(3x+3y)+(cy+cx)=3(x+y)+c(x+y)=(3+c)(x+y)
Объяснение: