![f(x)=tg^5\frac{3x}{5}\; \; ,\; \; f(x)=\Big(tg\frac{3x}{5}\Big)^5\\\\(u^5)'=5u^4\cdot u'\; \; ,\; \; u=tg\frac{3x}{5}\\\\f'(x)=5\cdot tg^4\frac{3x}{5}\cdot (tg\frac{3x}{5})'=\; \Big[\; (tgu)'=\frac{1}{cos^2u}\cdot u'\; ,\; u=\frac{3x}{5}\; \Big]=\\\\=5\cdot tg^4\frac{3x}{5}\cdot \dfrac{1}{cos^2\frac{3x}{5}} \cdot \Big(\dfrac{3x}{5}\Big)'=5\cdot tg^4\frac{3x}{5}\cdot \dfrac{1}{cos^2\frac{3x}{5}}\cdot \dfrac{3}{5}=\dfrac{3\cdot tg^4\frac{3x}{5}}{cos^2\frac{3x}{5}}](/tpl/images/1084/4316/fd638.png)
1)3b^2-10b-10/20b^4
2) 5x-5/x^2-25.
3) 2/x^2-3x
4) 1+6a/a+2
Объяснение:
1)Надо записать под общим знаменателем 20b^4. И подставлять в числитель. 5b*(3b-2)-2(6b^2-5)/20b^4. 15b^2-10b-12b^2+10/20b^4.
2) общий знаменатель x^2-25.
X-5+4x/x^2-25. 5x-5/x^2-25
3) рассписываем x^2-9 как (X-3)(X+3). И из x^2-3x выносим X. X(X-3). и общим знаменателем будет X(X-3)(X+3). Тогда:
4X-2X+6/X(X-3)(X+3). 2X+6/X(X-3)(X+3). 2(X+3)/X(X-3)(X+3). Сокращаем (X+3).
2/X^2-3X.
4) общий знаменатель a+2.
1-3a^2+3a^2+6a/a+2. -3a^2 и +3a^2 сокращаются. 1+6a/a+2
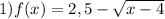
Выражение, стоящее под корнем чётной степени, должно быть неотрицательным, то есть ≥ 0 .
x - 4 ≥ 0
x ≥ 4
ответ : x ∈ [4 ; + ∞)
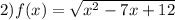
x² - 7x + 12 ≥ 0
(x - 3)(x - 4) ≥ 0
+ - +
____________[3]___________[4]_________
//////////////////////// ////////////////////
ответ : x ∈ (- ∞ ; 3] ∪ [4 ; + ∞)
3) Знаменатель дроби не должен равняться нулю, так как на ноль делить нельзя.
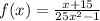
25x² - 1 ≠ 0
25x² ≠ 1
x² ≠ 1/25
x₁ ≠ - 1/5 x₂ ≠ 1/5
ответ : x ∈ (- ∞ ; - 1/5) ∪ (- 1/5 ; 1/5) ∪ (1/5 ; + ∞)