4. x = 1 ; 2 ; 3 ; 4
5. x =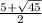 
; 
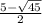; 3 ; 2
Объяснение:
4. (x² - 5x)(x² - 5x + 10) + 24 = 0
Произведем замену: (x² - 5x) = t
Тогда: t(t + 10) + 24 = 0
t² + 10t + 24 = 0
D = 10² - 4·24 = 100 - 96 = 4
; 
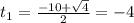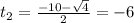
Произведем обратную размену: t = (x² - 5x)
• (x² - 5x) = -4
x² - 5x + 4 = 0
D = (-5)² - 4·4 = 25 - 16 = 9
; 
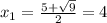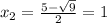
• (x² - 5x) = -6
x² - 5x + 6 = 0
D = (-5)² - 4·6 = 25 - 24 = 1
; 
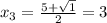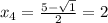
ответ: x = 1 ; 2 ; 3 ; 4
5. (x² - 5x + 2)(x² - 5x - 1) = 28
Произведем замену: x² - 5x = t
(t + 2)(t - 1) = 28
t² - t + 2t - 2 = 28
t² + t - 30 = 0
D = 1² - 4·(-30) = 1 + 120 = 121
; 
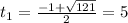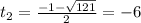
Произведем обратную размену: t = (x² - 5x)
• x² - 5x = 5
x² - 5x - 5 = 0
D = (-5)² - 4·(-5) = 25 + 20 = 45
; 
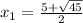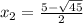
• (x² - 5x) = -6
x² - 5x + 6 = 0
D = (-5)² - 4·6 = 25 - 24 = 1
;
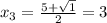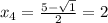
ответ: x = 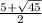; ; 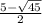3 ; 2
ответ:max y(x)=y(1)=6, min y(x)=y(-2)=-21
Объяснение: y' = (-x³+12x-5)' = -3x² +12x ⇒если y'=0, то -3x² +12x =0 ⇒ -3х(х-4) =0 ⇒ -3х=0 или х -4 =0 ⇒ х₁=0, х₂=4 -критические точки. Но х=4 ∉[-2;1], поэтому найдём значения функции в критической точке х=0 и на концах отрезка [-2;1]. у(0)= -0³+ 12·0 -5 = -5; у(-2) = - (-2)³ +12·(-2) -5 =8-24-5= -21 у(1) = -1³ +12·1+5= -1+12-5= 6. ⇒ max y(x)=y(1)=6, min y(x)=y(-2)=-21
90 кг.
Объяснение:
Пусть х кг - масса 30%-ного сплава,
тогда (120 - х) кг - масса 70%-ного сплава.
Масса меди в 30%-ном сплаве равна 0,3х кг,
а в 70%-ном сплаве - 0,7(120 - х) кг.
Полученный 40%-ый сплав содержит медь массой (120 · 0,4) кг.
0,3х + 0,7(120 - х) = 120 · 0,4
0,3х + 84 - 0,7х = 48
- 0,4х = 48 - 84
- 0,4х = - 36
0,4х = 36
х = 36 : 0,4
х = 90 (кг) - масса 30%-ного сплава.