a2 = 4; a4 = 28;
a2 = a1 + d(2 - 1) = a1 + d
a4 = a1 + d(4 - 1) = a1 + 3d
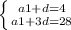
Выражаем a1 из системы:
a1 = 4 - d
4 - d + 3d = 28 (подставляем значение a1 во второе выражение, вместо a1)
Приводим подобные и переносим числа в право(со сменой знака на противоположный):
a1 = 4 -d; a1 = 4 - d
2d = 28 - 4; d = 12
ответ найдем: d = 12, можем перепроверить просто подставив соответствующие числа в арифметическую прогрессию:
a2 = 4; a3 = 4 + 12 = 16; a4 = 16 + 12 = 28; - ответ верен!
Объяснение: Для того, чтобы найти Разницу арифметической прогрессии (d), в данном случаи, нам нужно сначала составить систему уравнения, использую известную формулу для нахождения aₓ где x - любое натуральное число: aₓ = a1 + d(x - 1). В данной формуле,
(x - 1) означает, что мы берем номер от a и отнимаем единицу:
a4 = a1 + d(4 -1) = a1 + d(3) = a1 + 3d
Затем нужно составить, из получившегося, и решить систему уравнения.
1)
подставим x = 4 в уравнение:
3(4-1) = 5 + 4
3 * 3 = 9
9 = 9
равенство выполняется, значит 4 - является решением
2)
3(2z + 7) + 4 = 5(z-3)
6z + 21 + 4 = 5z - 15
6z + 25 = 5z - 15
6z - 5z = - 15 - 25
z = - 40
3)
а) наим = -1 наиб = 2
б) наим = -9 наиб = -1
4)
a)
2x - 71 <= 1
2x <= 1 + 71
2x <= 72
x <= 36
ответ : ( - ∞ ; 36]
б)
-3x >= 15
3x <= - 15
x <= -15/3
x <= -5
ответ : ( - ∞ ; -5]
5)
а) так как - 2 > - ∞ и -0.3 < + ∞ то ответ ( - 2 ; - 0.3)
б) так отрезок (0 ; 3 ) лежит целиком внутри [-5; 8) то ответ [-5; 8)