3) y = -1; 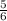 ; 1
; 1
4) Нет корней
Объяснение:
3) Прибавим левые и правые части уравнений системы:
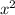 + 7xy + 9
+ 7xy + 9 - xy = 10 - 6
- xy = 10 - 6
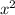 + 6xy + 9
+ 6xy + 9 = 4
= 4
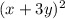 = 4
= 4
x + 3y = 2 x + 3y = -2
1) x = 2 - 3y 2) x = -3y - 2
По очереди подставим получившиеся значения х во второе уравнение:
1) 9 - (2 - 3y)y = 10
- (2 - 3y)y = 10
9 - 2y + 3
- 2y + 3 = 10
= 10
12 - 2y - 10 = 0
- 2y - 10 = 0
6 - y - 5 = 0
- y - 5 = 0
Решим через дискриминант:
a = 6 b = -1 c = -5
D = 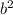 - 4ac = 1 + 120 = 121 =
- 4ac = 1 + 120 = 121 = 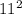
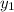 =
= 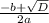 =
= 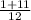 = 1
= 1
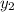 =
= 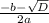 =
= 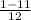 =
= 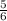
2) 9 - (- 3y - 2)y = 10
- (- 3y - 2)y = 10
9 + (3y + 2)y = 10
+ (3y + 2)y = 10
9 + 2y + 3
+ 2y + 3 = 10
= 10
12 + 2y - 10 = 0
+ 2y - 10 = 0
6 + y - 5 = 0
+ y - 5 = 0
Решим через дискриминант:
a = 6 b = 1 c = -5
D = 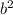 - 4ac = 1 + 120 = 121 =
- 4ac = 1 + 120 = 121 = 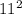
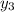 =
= 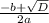 =
= 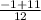 =
= 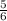
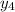 =
= 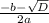 =
= 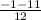 = -1
= -1
Корень 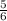 повторяется, а значит мы получили 3 различных корня:
повторяется, а значит мы получили 3 различных корня:
y = -1; 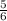 ; 1
; 1
4)
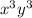 -
-  = -54
= -54
 = -18
= -18
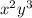 (x - y) = -54
(x - y) = -54
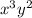 (x - y) = -18 => 3
(x - y) = -18 => 3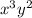 (x - y) = -54
(x - y) = -54
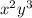 =
= 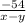
3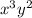 =
= 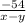
Следовательно:
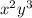 = 3
= 3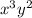
3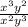 = 0
= 0
ОДЗ: х≠0, у≠0
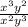 = 0
= 0
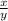 = 0
= 0
х = 0
Противоречие ОДЗ, значит система корней не имеет.
Объяснение:
Составить систему уравнений у меня не получилось
х деталей за час - производительность первого рабочего
(х-4) дет/час - производительность второго рабочего
48 : х + 1 = 48 : (х-4)
(48 + х)/х = 48/(х-4)
(48+х)(х-4) = 48х
48х + х² - 192 - 4х = 48х
48х + х² - 192 - 4х - 48х = 0
х² - 4х - 192 = 0
(Извините, не знаю каким в классе Вы решаете квадратные уравнения. Перехожу сразу к результату.)
х² - 16х + 12х - 192 = 0
х(х-16) +12(х-16) = 0
(х-16)(х+12) = 0
Первый корень уравнения:
х+12 = 0
х = -12 - ответ отрицательный
Второй корень:
х-16 = 0
х = 16 (дет/час) - производительность первого рабочего
ответ: Первый рабочий делает 16 деталей за час