Алгебра: разобраться , как решить, ответить. Как сделать

разобраться , как решить, ответить. Как сделать

👇

Открыть все ответы

Ответ:

Nikitos220220

05.07.2020

36(x-1)^4 + 26x = 13x^2 + 12
36(x-1)^4 - 13x^2 + 26x - 12 = 0
36(x^4 - 4x^3 + 6x^2 - 4x + 1) - 13x^2 + 26x - 12 = 0
36x^4 - 144x^3 + 216x^2 - 144x + 36 - 13x^2 + 26x - 12 = 0
36x^4 - 144x^3 + 203x^2 - 118x + 24 = 0
Разложим так
36x^4 - 18x^3 - 126x^3 + 63x^2 + 140x^2 - 70x - 48x + 24 = 0
18x^3*(2x-1) - 63x^2*(2x-1) + 70x*(2x-1) - 24*(2x-1) = 0
(2x-1)(18x^3 - 63x^2 + 70x - 24) = 0
x1 = 1/2
Теперь разложим кубическое уравнение
18x^3 - 12x^2 - 51x^2 + 34x + 36x - 24 = 0
6x^2*(3x-2) - 17x*(3x-2) + 12(3x-2) = 0
(3x-2)(6x^2 - 17x + 12) = 0
x2 = 2/3
И, наконец, решаем квадратное уравнение
D = 17^2 - 4*6*12 = 289 - 288 = 1
x3 = (17 - 1)/12 = 16/12 = 4/3
x4 = (17 + 1)/12 = 18/12 = 3/2
ответ: 1/2; 2/3; 4/3; 3/2

4,4(66 оценок)

Ответ:

aleXxxx03

05.07.2020

Объяснение:

Задача №1

Расстояние по течению - 4 км

Расстояние против течения - 3 км

Собственная скорость - х км/час

Скорость течения - 3 км/час

Значит

скорость движения по течению (х+3) км/час

скорость движения против течения ( х-3) км/час

Соответственно время движения по течению 4/(х+3) час.

против течения : 3/(х-3) час

По условию , на путь по течению потрачено на 4 мин. меньше

4 мин.= 4/60= 1/15 часа

Составим уравнение:

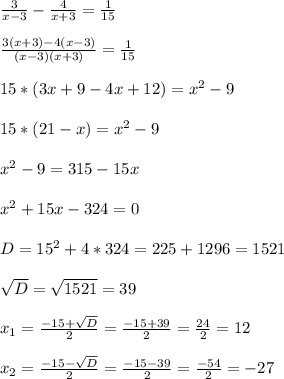
$\frac{3}{x-3} -\frac{4}{x+3}=\frac{1}{15} \\ \\ \frac{3(x+3)-4(x-3)}{(x-3)(x+3) } =\frac{1}{15}\\ \\ 15*(3x+9-4x+12)= x^{2} -9\\ \\ 15*(21-x)= x^{2} -9\\ \\ x^{2} -9=315-15x\\ \\ x^{2} +15x-324=0 \\ \\ D=15^{2} +4*324= 225+1296= 1521\\ \\ \sqrt{D} =\sqrt{1521}=39\\ \\ x_{1} =\frac{-15+\sqrt{D} }{2}= \frac{-15+39}{2}=\frac{24}{2}= 12 \\ \\ x_{2} =\frac{-15-\sqrt{D} }{2}= \frac{-15-39}{2}= \frac{-54}{2}=-27$

Корень х₂= -27 не подходит , поскольку скорость не может быть отрицательной , значит

собственная скорость буксира 12 км/час

Задача №2

Найдем расстояние , которое составили 8/15 пути

225*8/15 = 120 км

Найдем расстояние , которое осталось

225-120=105 км

х км/ч - скорость автомобиля на первом участке пути,

(х-10) км/час - скорость автомобиля на втором участке пути, тогда время, которое потратил автомобиль на 1-й участок пути составит

120/х час, значит на второй участок потратил

105/(х-10) час

Общее время составило 3 часа .

Можем составить уравнение:

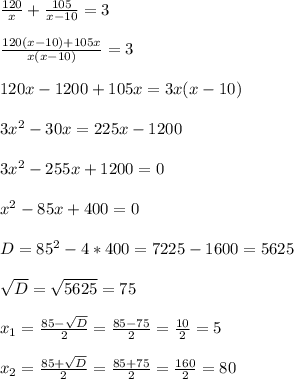
$\frac{120}{x}+ \frac{105}{x-10}= 3 \\ \\ \frac{120(x-10)+ 105x}{x(x-10)}=3\\ \\ 120x-1200+105x=3x(x-10)\\ \\ 3x^{2} -30x=225x-1200\\ \\ 3x^{2} -255x+1200=0\\ \\ x^{2} -85x+400=0 \\ \\ D= 85^{2}-4*400= 7225-1600=5625\\ \\ \sqrt{D}=\sqrt{5625}=75\\ \\ x_{1} =\frac{85-\sqrt{D} }{2}= \frac{85-75}{2}= \frac{10}{2}= 5 \\ \\ x_{2}=\frac{85+\sqrt{D} }{2}=\frac{85+75}{2}=\frac{160}{2}= 80$