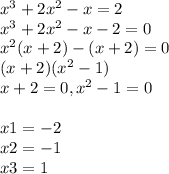В данном уравнении у нас есть две переменные - х и у. Для нахождения значения выражения ху+у^2/28х•7х/х+у при заданных значениях х=7,8 и у=-2, нам нужно подставить эти значения вместо переменных и произвести вычисления.
Давайте начнем с подстановки значений. Заменим х и у в исходном выражении:
x = 7,8, y = -2
Теперь пошагово решим это выражение:
1. Подставляем значения х и у: 7,8*(-2) + (-2)^2 / (28 * 7 * 7 / 7 + (-2)).
2. Вычисляем сначала значения в скобках 7 * 7: 28 * 1 + (-2).
3. Далее умножаем получившееся значение на 28: 28 + (-2).
4. Получаем значение в скобках: 26.
5. Теперь посчитаем -2^2, возводя -2 в квадрат: 4.
6. Теперь подставим полученные значения в основное выражение: 7,8*(-2) + 4 / 26.
7. Умножаем 7,8 на -2: -15,6 (+ если умножение положительно, - если отрицательно).
8. Делим 4 на 26: 0,153 (последующие десятичные разряды будут округлены, если требуется).
9. Складываем полученные результаты: -15,6 + 0,153 = -15,447.
Таким образом, значение выражения ху+у^2/28х•7х/х+у при х=7,8 и у=-2 равно -15,447.
Если у школьника возникнут еще вопросы или потребуется дополнительное объяснение, я готов помочь!
Для решения данной задачи будем использовать алгебраический подход.
Пусть первое натуральное число будет равно Х. Тогда второе натуральное число будет равно Х + 1, так как они являются последовательными числами.
Сумма квадратов этих чисел задается следующим выражением: Х^2 + (Х + 1)^2, где Х^2 обозначает квадрат первого числа, а (Х + 1)^2 - квадрат второго числа.
Произведение этих чисел задается выражением: Х * (Х + 1), где Х обозначает первое число, а (Х + 1) - второе число.
Согласно условию задачи, сумма квадратов этих чисел на 111 больше их произведения. То есть, Х^2 + (Х + 1)^2 = Х * (Х + 1) + 111.
Решим полученное уравнение:
Х^2 + Х^2 + 2Х + 1 = Х^2 + Х + 111.
Сократим одинаковые слагаемые на обеих сторонах уравнения:
2Х^2 + 2Х + 1 = Х^2 + Х + 111.
Перенесем все слагаемые на одну сторону:
2Х^2 + 2Х + 1 - Х^2 - Х - 111 = 0.
Упростим уравнение:
Х^2 + Х - 110 = 0.
Уравнение является квадратным трехчленом и может быть решено с помощью формулы дискриминанта. Дискриминант D равен: D = b^2 - 4ac, где a, b и c - коэффициенты при соответствующих степенях Х.
В нашем уравнении a = 1, b = 1, c = -110.
Вычислим дискриминант:
D = 1^2 - 4 * 1 * -110 = 1 + 440 = 441.
Значение дискриминанта равно 441.
Теперь применим формулу для нахождения корней квадратного уравнения:
Х = (-b +- sqrt(D)) / (2a).
Так как в задаче исключены отрицательные числа, полученный отрицательный корень не подходит. Поэтому первое натуральное число равно 10, а второе натуральное число будет равно 10 + 1 = 11.
Итак, два последовательных натуральных числа, сумма квадратов которых на 111 больше их произведения, равны 10 и 11.
Відповідь:
Пояснення:
1)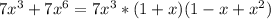
2)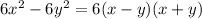
3)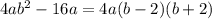
4)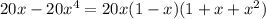
5)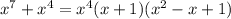
6)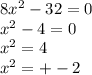
7)