Дана функция: y = х2 - 4х -5 запишите координаты вершины параболы; определите, в каких четвертях находится - id1094487620230326 от Лизавеликая111 26.03.2023 06:28

Question

Алгебра: Дана функция: y = х2 - 4х -5 запишите координаты вершины параболы; определите, в каких четвертях находится график функции; запишите ось симметрии параболы; найдите точки пересечения графика с осями координат; постройте график функции.

Лизавеликая111 · Accepted Answer

Для начала выразим в данном уравнении одну переменную через другую. Например, переменную через переменную .

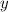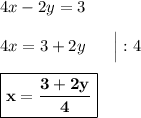
$4x - 2y = 3\\\\4x = 3 + 2y\ \ \ \ \ \Big| :4\\\\\boxed{\bf{x = \dfrac{3+2y}{4}}}$

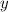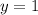Для каждой пары решений этого уравнения данное равенство будет выполняться. Теперь берём для переменной любое значение, которое захотим, подставляем в выражение сверху и находим переменную . Возьмём, например, y = 1 , получится:

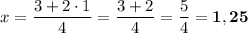$x = \dfrac{3+2\cdot 1}{4} = \dfrac{3+2}{4} = \dfrac{5}{4} = \bf{1,25}$ .

Таким образом, пара чисел 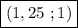$\boxed{(1,25\ ;1)}$ является решением нашего уравнения. Подставим, например, y = -1 :

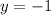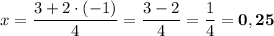$x = \dfrac{3+2\cdot (-1)}{4} = \dfrac{3-2}{4} = \dfrac{1}{4} = \bf{0,25}$ .

И ещё одну пару чисел, 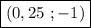$\boxed{(0,25\ ;-1)}$ , мы получили. И для последней пары мы возьмём, к примеру, y = 5 :

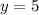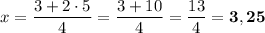$x = \dfrac{3+2\cdot 5}{4} = \dfrac{3+10}{4} = \dfrac{13}{4} = \bf{3,25}$ .

И получили последнюю пару чисел: 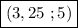$\boxed{(3,25\ ;5)}$ .

MOGZ ответил