Дана арифметическая прогрессия (an). Известно, что a1=3,1 и d=0,6.
Вычисли сумму первых тринадцати членов арифметической прогрессии.

Запиши ответ в виде числа, при необходимости округлив его до десятых

👇

Увидеть ответ

Ответ:

Anastasiua005

30.01.2021

Для начала найдем 13-ый член:

a₁₃=a₁+(n-1)d=3,1+(13-1)·0,6=3,1+12·0,6=10,3

Найдем сумму первых 13-ти членов:

S₁₃=n·(a₁+aₙ)/2=13·(3,1+10,3)/2=87,1

ответ: S₁₃=87,1.

4,7(82 оценок)

Открыть все ответы

Ответ:

Виолетта2018

30.01.2021

Как-то кривенько все получается, либо приблизительно, либо с корнями...

Ну смотрите сами.

1. А+В = 5

А*В = -2

Выражаем А через В

А = (5-В) и подставляем во второе выражение

(5-В)* В = -2, раскрываем скобки и получаем кв. уравнение

В в кв - 5В - 2= 0, по формуле находим корни В1 В2

В1 = ( 5- кв корень(25+8)):2 = 2.5 - кв корень(33)/2

В2 = ( 5 + кв корень(25+8))/2 = 2.5 + кв корень(33)/2

Потом находим А1 и А2

А1 = 5 - (2.5 - кв корень(33)/2) = 2.5 + кв корень (33)/2

А2 = 5 - (2.5 + кв корень(33)/ 2) = 2,5 - кв корень(33)/2

Теперь ищем (А-В) в кв (А1-В1) и (А2-В2)

1. ((2.5+кв к(33)/2)-(2.5-кв.к(33)/2)в кв =( кв к(33))в кв = 33

2. ((2.5-кв к(33)/2)- (2,5+кв к(33)/2)в кв = (-кв к(33))в кв = 33

Проверьте, может где-то перемудрила, но основная мысль такова.

Удачи!

4,4(52 оценок)

Ответ:

Кристалина12

30.01.2021

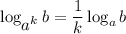1) а) По свойству $\log_\big{a^k}b=\dfrac{1}{k}\log_ab$ имеем , что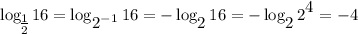
$\log_\big{ \frac{1}{2} }16=\log_\big{2^{-1}}16=-\log_\big{2}16=-\log_\big{2}2^\big{4}=-4$

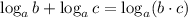б) Используя свойство $\log_ab+\log_ac=\log_a(b\cdot c)$ , получим что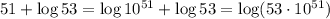
$51+\log53=\log10^{51}+\log53=\log(53\cdot 10^{51})$

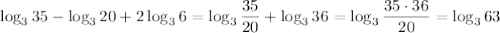
в) $\log_335-\log_320+2\log_36=\log_3 \dfrac{35}{20} +\log_336=\log_3 \dfrac{35\cdot 36}{20} =\log_363$

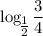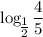
Задание 2. Сравнить числа: $\log_\big{ \frac{1}{2} } \dfrac{3}{4}$ и $\log_\big{ \frac{1}{2} } \dfrac{4}{5}$

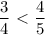Поскольку $\dfrac{3}{4} \ \textless \ \dfrac{4}{5}$ , то в силу монотонности функции( 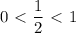$0\ \textless \ \dfrac{1}{2} \ \textless \ 1$ функция убывающая) имеем что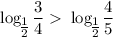
$\log_\big{ \frac{1}{2} } \dfrac{3}{4}\ \textgreater \ \log_\big{ \frac{1}{2} } \dfrac{4}{5}$

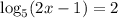
Задание 3. Решить уравнение $\log_5(2x-1)=2$
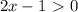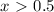
ОДЗ уравнения: $2x-1\ \textgreater \ 0$ откуда $x\ \textgreater \ 0.5$
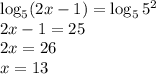
$\log_5(2x-1)=\log_55^2\\ 2x-1=25\\ 2x=26\\ x=13$

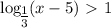
Задание 4. Решить неравенство $\log_\big{ \frac{1}{3} }(x-5)\ \textgreater \ 1$
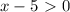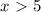
ОДЗ: $x-5\ \textgreater \ 0$ откуда $x\ \textgreater \ 5$
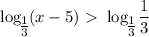
$\log_\big{ \frac{1}{3} }(x-5)\ \textgreater \ \log_\big{ \frac{1}{3} } \dfrac{1}{3}$
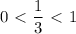Поскольку основание $0\ \textless \ \dfrac{1}{3} \ \textless \ 1$ , функция убывающая, то знак неравенства меняется на противоположный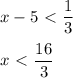
$x-5\ \textless \ \dfrac{1}{3} \\ \\ x\ \textless \ \dfrac{16}{3}$

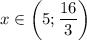
С учетом ОДЗ получим окончательный ответ $x \in \bigg(5; \dfrac{16}{3}\bigg)$

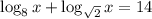
Задание 5. Решить уравнение $\log_8x+\log_{ \sqrt{2} }x=14$
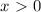
ОДЗ уравнения $x\ \textgreater \ 0$
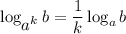Используя свойство $\log_\big{a^k}b=\dfrac{1}{k}\log_ab$ , получим что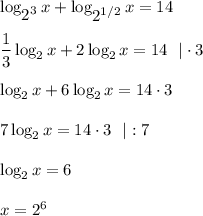
$\log_\big{2^3}x+\log_\big{2^{1/2}}x=14\\ \\ \dfrac{1}{3} \log_2x+2\log_2x=14~~|\cdot 3\\ \\ \log_2x+6\log_2x=14\cdot 3\\ \\ 7\log_2x=14\cdot 3~~|:7\\ \\ \log_2x=6\\ \\ x=2^6$

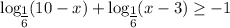
Задание 6. Решить неравенство $\log_\big{ \frac{1}{6} }(10-x)+\log_\big{ \frac{1}{6} }(x-3)\geq -1$
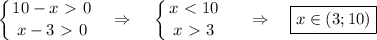
ОДЗ $\displaystyle \left \{ {{10-x\ \textgreater \ 0} \atop {x-3\ \textgreater \ 0}} \right. ~~\Rightarrow~~~ \left \{ {{x\ \textless \ 10} \atop {x\ \textgreater \ 3}} \right. ~~~~\Rightarrow~~~ \boxed{x\in (3;10)}$

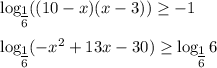
$\log_\big{ \frac{1}{6} }((10-x)(x-3))\geq -1\\ \\ \log_\big{ \frac{1}{6} }(-x^2+13x-30)\geq \log_\big{ \frac{1}{6} }6$
В силу монотонности функции логарифма имеем что
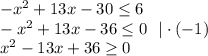
$-x^2+13x-30\leq 6\\ -x^2+13x-36\leq 0~~|\cdot(-1)\\ x^2-13x+36\geq 0$
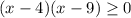$(x-4)(x-9)\geq 0$ (*)
Решением последнего неравенства (*) есть $x \in (-\infty;4]\cup[9;+\infty)$

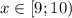С учетом ОДЗ $x \in [9;10)$ - ОТВЕТ.

Задание 7. Решить неравенство $\log_3^2x-2\log_3x \leq 3$
ОДЗ неравенства $x\ \textgreater \ 0$
Представим левую часть неравенства в следующем виде:
$\log_3^2x-2\log_3x+1\leq 4\\ \\ (\log_3x-1)^2\leq 4\\ \\ |\log_3x-1|\leq 2\\ \\ -2\leq \log_3-1\leq 2~~|+1\\ \\ -1\leq \log_3x\leq 3$

Имеем совокупность неравенств $\left[\begin{array}{ccc}\log_3x\geq -1\\ \log_3x\leq 3\end{array}\right~~~\Rightarrow~~~~~ \left[\begin{array}{ccc}x \geq \dfrac{1}{3}\\ x\leq 27 \end{array}\right$

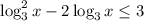
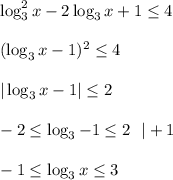
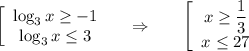
И с учетом ОДЗ мы получим ответ $x \in \bigg[\dfrac{1}{3} ;27\bigg].$