найти площадь криволинейной трапеции!
Задание 1.
Найти площадь криволинейной трапеции f(x)=x^2, ограниченную линиями x=1 и x=3. Построить.
Задание 2.
Найти площадь криволинейной трапеции f(x)=sinx, ограниченную линиями x=0 и x=π. Построить.
Задание 3.
Найти площадь криволинейной трапеции f(x)=cosx, ограниченную линиями x=0 и x=π/2. Построить.
Задание 4.
Найти площадь криволинейной трапеции f(x)=x^3, ограниченную линиями x=2 и x=4. Построить.
Задание 5.
Найти площадь криволинейной трапеции f(x)=x^2-4x+5, ограниченную линиями y=0, x=1 и x=3. Построить.
Задание 6.
Найти площадь криволинейной трапеции f(x)=1+1/2 cosx, ограниченную линиями y=0, x=-π/2 и x=π/2. Построить.
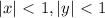
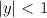 возвести в квадрат, получив,
возвести в квадрат, получив, 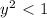 , что и требовалось проверить.
, что и требовалось проверить.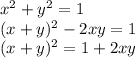
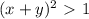
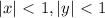 , следует, что 0 <x < 1, 0 < y < 1
, следует, что 0 <x < 1, 0 < y < 1
Отсюда легко убедиться в справедливости неравенства под номером 2. Для этого достаточно обе части неравенства
Первое неравенство можно проверить, например, следующим образом. Представим первое равенство следующим образом:
Поскольку x > 0, y > 0, то 2xy > 0, а 1 + 2xy > 1. Значит, и
Поскольку x + y > 0, то из последнего неравенства следует неравенство x + y > 1, что и требовалось доказать.
Последние два неравенства неверные. Сначала заметим, что из неравенства
Можно доказать, что куб таких чисел меньше квадрата, в третьем же неравенстве наоборот всё.
Аналогично, куб числа от 0 до единицы всегда меньше самого числа. Эти утверждения очевидны. Поэтому неравенства 3 и 4 неверны. Выбрать какой-то один вариант тут не получится.