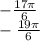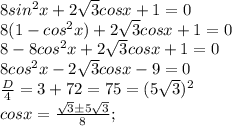
Так как функция косинус по модулю не превосходит единицы в поле действительных чисел, то выбираем 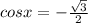
Далее решаем это уравнение:
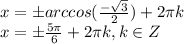
По условию нужно найти корни на промежутке ![[-\frac{7\pi}{2}; -2\pi]](/tpl/images/1359/8515/36df4.png) .
.
Это можно сделать несколькими например, с неравенства:
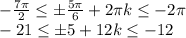
Рассмотрим случай, когда 5 имеет знак "плюс":
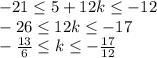
Очевидно, что из целых k подходит k = -2.
Теперь рассмотрим случай, когда 5 имеет знак "минус":
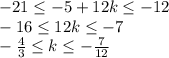
k = -1 нам подходит.
Теперь подставляем полученные k в серию корней:
1) Когда плюс - k = -2, т. е. 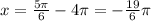
2) Когда минус - k = -1, т. е. 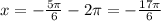
ответ: а) 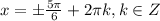
б)