Составляем системы уравнений во всех случаях:
a)
m + n = 4
mn = 4
(Шаг 1) Выражаем в первом уравнении m через n и подставляем во второе:
m = 4 - n
(4 - n)n = 4
(Шаг 2) Теперь работаем со вторым уравнением:
-n² + 4n - 4 = 0 | * -1
n² - 4n + 4 = 0
D = 16 - 16 = 0
n = 4/2 = 2
(Шаг 3) Подставляем получившийся корень (если D > 0, то корней будет 2, подставляем оба и получаем две пары решений) в первое уравнение системы:
m = 4 - 2
m = 2
ответ: m = 2; n = 2.
b)
m + n = -5
mn = 6
Шаг 1:
m = -5 - n
(-5 - n)n = 6
Шаг 2:
-5n - n² - 6 = 0 | * -1
n² + 5n + 6 = 0
D = 25 - 24 = 1
n1 = (-5 + 1)/2 = -2
n2 = (-5 - 1)/2 = -3
Шаг 3:
m1 = -5 - (-2)
m1 = -5 + 2
m1 = -3
m2 = -5 - (-3)
m2 = -5 + 3
m2 = 2
ответ: m1 = -3; n1 = -2; m2 = -2; n2 = -3
Таким же образом решаются следующие два уравнения.
1)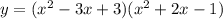
2)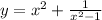
3)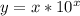
4)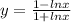
5) y = arctgx - arcctgx
6)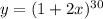
7)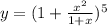
8)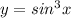
9) y = lncosx