7–10. Два уравнения называют равносильными, если они имеют одинаковые корни или если оба уравнения не имеют корней. Решаем уравнения, находим корни уравнения и сравниваем ответы.
7. 1) 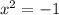
число в корне не может равняться отрицательному числу, корней уравнения нет.
2) 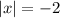
число в модуле не может равняться отрицательному числу, корней уравнения нет.
=> уравнения равносильные.
8. 1) 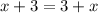
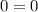
корней уравнения нет.
2) 
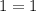
корней уравнения нет.
=> уравнения равносильные.
9. 1) 
ОДЗ: 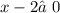 ,
, 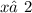 ;
;
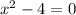
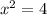
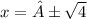
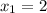 (не удовлетворяет ОДЗ),
(не удовлетворяет ОДЗ), 
ответ: 
2) 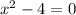
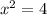
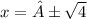
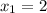 ,
, 
ответ:  ;
; 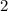
=> уравнения не равносильные.
10. 1) 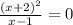
ОДЗ: 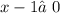 ,
, 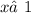 ;
;
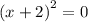
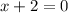

ответ: 
2) 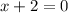

ответ: 
=> уравнения равносильные.

12–16. Необходимо найти сумму корней уравнения. Решаем уравнение, находим корни уравнения, складываем их. Если уравнение имеет один корень, то суммой (ответом) будет значение корня уравнения.
12. 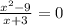
ОДЗ: 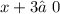 ,
,  ;
;
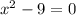


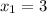 ,
,  (не удовлетворяет ОДЗ)
(не удовлетворяет ОДЗ)
ответ: 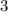
13. 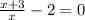
ОДЗ: 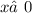 ;
;
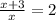
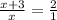
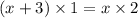
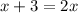
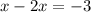
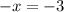
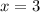
ответ: 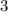
14. 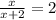
ОДЗ:  ,
,  ;
;
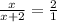
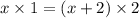

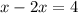


ответ: 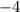
15. 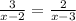
ОДЗ: 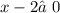 ,
, 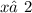 ,
, 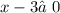 ,
,  ;
;
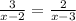
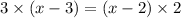
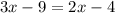
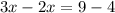
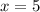
ответ: 
16. 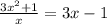
ОДЗ: 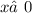 ;
;
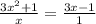
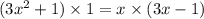
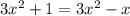
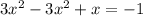

ответ: 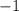
Результат - двойка, возведенная в нечетную степень - не точный квадрат. Однако, если степень будет четной, то число окажется точным квадратом:
Для получения такого числа достаточной вычеркнуть из исходного набора любое число с нечетным показателем. Тогда по правилу деления степеней в показателе окажется разность нечетных чисел, то есть число четное. Выбрать же некоторое число с нечетной степенью можно так как в исходном наборе и чисел с нечетной степенью и чисел с четной степенью одинаковое количество.
ответ: 1009