А) 2х^2+5х+4 = 0 Б) 9х^2+4х+1 = 0 В) х^2-4х+4 = 0
Д = 25-4*2*4 = -7 Д = 16-4*9*1 = -20 Д = 16-4*1*4 = 0
-7 < 0 нет решений -20 < 0 нет решений х1,2 = 2 один корень
Г) х^2-7х+5 = 0
Д = 49-4*1*5 = 29
х1 = (7+ корень из 29)/2
х2 = (7- корень из 29)/2
ответ: Г)
Y= - 2,5X - 6
Объяснение:
Чертим график лин. ФУНК. y=-3x+1 и ставим точку с координатами (-2; - 1).
Через эту точку проводим прямую перпендикулярно линейной функции y=-3x+1.
Формула линейной функции равна y=kx+m, теперь находим две точки на графике второй лин фун 1) с координатами (0; - 6), 2) с координатами (-2; - 1). Поставляем в формулу лин фун координаты точки 1) и получается - 6=0k+ m то есть m=-6.
Мы нашли m. Теперь k. Поставляем в формулу лин фун координаты точки 2) и m и получается - 1=-2k - 6 то есть 2k=-5 то есть k=-2,5. Мы узнали k и m. Поставляем их в формулу лин фун и получается y= - 2,5x - 6. Готово!
Если что, лин фун это линейная функция
Я понятно объяснил?
ctgx(ctgx+1)=0
ctgx=0 или ctgx+1=0
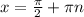ctgx=-1
n=-1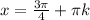 
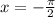k=-1
n=0 
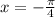
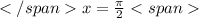k=0
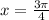
т.е. на данном промежутке находятся 4 корня
2x2 + 5x + 4 = 0
D = b2 - 4ac
D = 25 - 32 = -7 < 0
ответ: нет решений
9x2 + 4x + 1 = 0
D = b2 - 4ac
D = 16 - 36 = -20 < 0
ответ: нет решений
x2 - 4x + 4 = 0
D = b2 - 4ac
D = 16 - 16 = 0
x = - b/2a
x = 4 /2= 2
ответ: x = 2
x2 - 7x + 5 = 0
D = b2 - 4ac
D = 49 - 20 = 29 = (√29)^2
x1,2 = -b ± √D/2a
x1 = 7 + √29/2
x2 = 7 - √29/2
ответ: x1 = 7 + √29/2 ; x2 = 7 - √29/2
ОТВЕТ -Г