Много 1. постройте график функции: а) y = 2(x − 2)2 + 2; б) y = −3x2 + 6x + 2, в) y = −2(x + 2)2 – 2; г) y = 3x2 + 6x + 1,2. а) найдите наибольшее и наименьшее значения функции y = −x2 + 2x + 3 на отрезке [0; 2]. б) найдите наибольшее и наименьшее значения функции y = 2x2 + 4x − 1 на отрезке
[−1; 3].3. решите графически уравнение а) х2 – 2х – 8 = 0, б) х2 – х – 6 = 0.
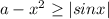
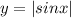расположен выше оси ОХ. 
.
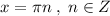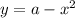- это параболы , ветви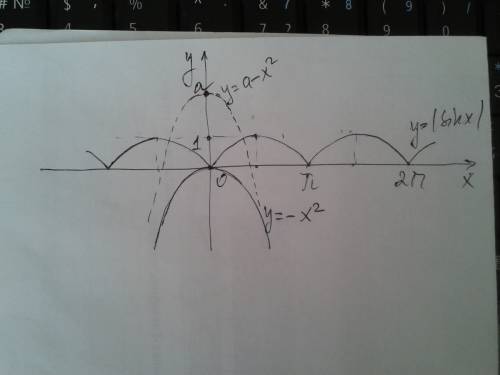
89 км/ч→ 56 км\ч→
АB - - - - - С
99 км
Допустим, машины встретились в точке С. На это им потребовалось одинаковое время t, за которое они разные пути S₁ и S₂:
S₁ = AB + BC = 99+BC
S₂ = BC
С другой стороны
S₁= v₁t = 89t
S₂ = v₂t = 56t
Выразим неизвестное время t из первого и второго уравнений и приравняем полученные выражения (поскольку время одно и то же) :
99+BC = 89t, t = (99+BC) / 89
BC = 56t, t = BC / 56
(99+BC) / 89 = BC / 56
56(99+BC) = 89 BC
5544 + 56 BC = 89 BC
5544 = 33 BC
BC = 5544 / 33 = 168
BC = 168 (км)
t = BC/56 = 168/56 = 3 (ч)
ответ: на расстоянии 168 км от города B через 3 часа после выезда
Можно решить другим
Представим, что вторая машина стоит в городе B.
Тогда первая машина движется к ней со скоростью
89-56 = 33 км/ч
Расстояние между машинами 99 км.
И это расстояние будет пройдено первой машиной за
время = путь / скорость = 99/33=3 ч.
Зная время, можно перейти к первоначальным условиям задачи (обе машины движутся) и найти расстояние между точками B и C. Это удобнее сделать, исходя из движения второй машины, потому что она двигалась из точки B в точку C.
длина BC = скорость второй машины * 3 часа = 56 км/ч * 3 ч = 168 км.