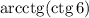
Известно соотношение:
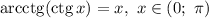
Кроме этого, известно, что основной период котангенса равен 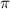 :
:
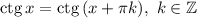
Таким образом, аргумент 6 нужно заменить некоторым аргументом вида 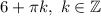 , чтобы с одной стороны котангенсы этих аргументов были равны, а с другой стороны полученный аргумент удовлетворял формуле для простого нахождения арккотангенса от котангенса.
, чтобы с одной стороны котангенсы этих аргументов были равны, а с другой стороны полученный аргумент удовлетворял формуле для простого нахождения арккотангенса от котангенса.
Запишем неравенство:
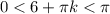
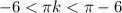
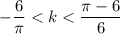
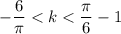
Выполним оценку обеих частей неравенства:
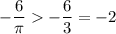
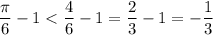
Получим:
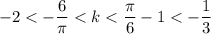
Или записывая соотношение для k:
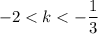
Единственное подходящее целое значение: 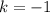 .
.
Запишем:
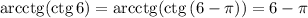
Действительно,  , арккотангенс может принимать такое значение.
, арккотангенс может принимать такое значение.
ответ: 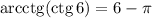
б. значение аргумента при у=-5:
-2х+5 = -5 2х = 10 х = 5.
в. Чтобы узнать, принадлежит ли графику функции точки А(1;3)В(-1;6), надо подставить в формулу значение аргумента х1 = 1, х2 = -1 и сравнить значение функции и ординату точки.
Если совпадают - то точка принадлежит графику функции.
у1 = -2*1 + 5 = -2 + 5 = 3 - совпадают.
у2 = -2*(-1) + 5 = 2 + 5 = 7 - не совпадают.
2) График функции У=3х+4 - это прямая линия.
Координаты точек пересечения графика с осями координат определяются приравниванием х или у нулю.
3*0+4 = 4 = точка пересечения оси ординат (ось у)
3х+4 = 0 3х = -4 х = -4/3 = -1(1/3) - точка пересечения оси абсцисс (ось х).
3) График функции у=кх проходит через начало координат.
Коэффициент к = dy/dx = -6 / 2 = -3.
График проходит через 0 и заданную точку.
4) Точка пересечения графиков определяется решением уравнения
-4х +1,3 = х - 2,7
5х = 4
х = 4/5 = 0,8
Вторая координата находится подстановкой полученного значения х в формулу одной из прямых у = -4*0,8 + 1,3 = -3,2 + 1,3 = -1,9
или у = 0,8 - 2,7 = -1,9.
5) Параллельные графики имеют равные коэффициенты при х:
графику У=-3х+12 параллельна прямая У=3х-5.