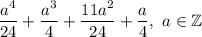
Преобразуем выражение:
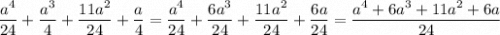
Рассмотрим и преобразуем числитель:
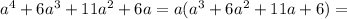
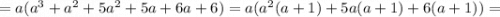
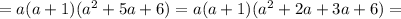
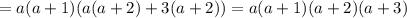
Получилось произведение четырех подряд идущих целых чисел.
Из четырех подряд идущих целых чисел гарантированно найдется хотя бы одно, кратное 3. Также, из четырех подряд идущих целых чисел найдется два четных числа, одно из которых не только четное, но и кратно 4.
Таким образом, в произведении гарантированно есть множители 3, 2 и 4. Тогда, такое произведение делится на 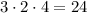 .
.
Запишем:
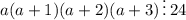
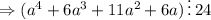
В исходной дроби такое выражение как раз делится на 24. Как выясняется, это выражение кратно 24. Значит, результат деления на 24 будет целым числом:
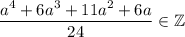
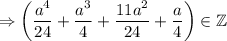
Доказано.
КЛАССИФИКАЦИЯ: Линейное неоднородное дифференциальное уравнение второго порядка со специальной право частью
Найти нужно: yо.н. = уо.о. + уч.н.
Найдем уо.о. (общее однородное)
Применим метод Эйлера
Пусть
Корни которого
Тогда общее решение однородного уравнения будет
Найдем теперь уч.н.(частное неоднородное)
где
Сравнивая
уч.н. =
Чтобы определить коэффициенты А и В, воспользуемся методом неопределённых коэффициентов:
Подставим в исходное уравнение и приравниваем коэффициенты при одинаковых х
Тогда частное решение неоднородного будет иметь вид
уч.н.
Запишем общее решение исходного уравнения