Пусть скорость первого велосипедиста - x км/ч. Тогда скорость второго - (x+3) км/ч. 1ый велосипедист проехал всё расстояние равное36 кмза (36/x) часов. 2ой проехал это расстояние за (36/(x+3)) часов. Известно, что 2ой велосипедист проехал расстояние на 1 час быстрее. Уравнение: 36/x-36/(x+3)=1 36(x+3)-36x=x(x+3) 36x+108-36x=x^{2}+3x x^2+3x-108=0 D=9+4*108=441=21^2 x1=(-3+21)/2=9 x2=(-3-21)/2=-12<0 не подходит 2) 9+3=12(км/ч) ответ: Скорость первого велосипедиста равна9 км/ч, а второго-12 км/ч.
Объяснение:
2.
a) 3x+12>4x-1 | (-x>-13) /-1 | x<13
7-2x<=10-3x | -3 <= -x /-1 | x <= 13. x принадлежит (-∞; 13].
б) 2x-9 > 6x+1 | (-4x > 10) / -4 | x<10
( -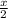 < 2 ) *-2 | x > 4. x принадлежит (-∞; 10) и (4; +∞).
< 2 ) *-2 | x > 4. x принадлежит (-∞; 10) и (4; +∞).
3.
а)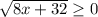 Взводим все в квадрат
Взводим все в квадрат
8x+32 => 0
8x => 32 делим все на 8
x => 4. x принадлежит [4; +∞).
б)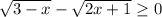 Взводим все в квадрат
Взводим все в квадрат
3-x-2x+1 => 0
4 => 3x Делим все на 3
1.3 => x
x <= 1.3. x принадлежит [-∞; 1.3).
4.
а-7 => 0 3-2a => 0
a => 7 3 => 2a
1.5 => a ответ: a принадлежит [7; +∞).