1. (6;-1) 2. (5; -1) 3. (-3;13) 4.(-3.5;-1) 5. (-1;2).
Объяснение:
1. Сложим 2 уравнения. y сократиться и получим:
2x=12
x=6.
Подставим полученный x=6 в любое уравнение системы (например в первое, получим уравнение относительно y , которое решим:
6+y=5;
y=5-6;
y= -1.
2. Домножим обе части первого уравнения на 5. Получим систему:
5x+5y=20;
3x-5y=20.
Сложим два уравнения, 5y и -5y сократятся дав в сумме 0.
получим уравнение относительно x:
8x=40;
x=5.
Подставляем x=5 например в первое уравнение:
5+y=4;
y=4-5;
y=-1.
3. 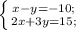
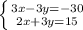
Складываем два уравнения:
5x=-15
x=-3
3-y=-10
-y=-10-3
y=10+3
y=13.
4. Первое ур-е умножим обе части на 3 а второе ур-е умножим обе части на -2.
Получим новую систему:
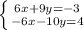
9y-10y=-3+4
-y=1
y=-1.
Подставляем в первое уравнение исходной системы y=2.
2x+3*2=-1
2x+6=-1
2x=-1-6
2x=-7
x=-3.5.
5. 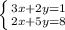
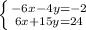
-4y+15y=-2+24;
y=2.
3x+2*2=1;
3x+4=1;
3x=1-4;
3x=-3;
x=-1.
Задача: Моторний човен пройшов 8 км за течією річки і 5 км проти течії, затративши на весь шлях 1 год. Знайти швидкість човна у стоячій воді, якщо швидкість течії річки дорівнює 3 км/год.
Рішення: Нехай х км/год — швидкість човна в стоячій воді, тоді швидкість човна за течією — х+3 км/год, а проти течії — х-3 км/год. Човен пройшов 8 км за течією 8/(х+3) год, а проти течії — 5/(х-3) год. Весь шлях човен пройшов за 1 год. Складемо і вирішимо рівняння.
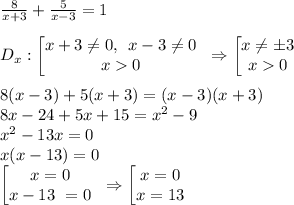
Відповідь: Швидкість човна у стоячій воді дорівню 13 км/год.
y=5/√7x+3-1/|x|-2
0=5/√7x+3 -1/|x|-2
5/√7x+3-1/|x|-2=0
5(|x|-2)-√7x+3/√7x+3*(|x|-2)=0
5(|x|-2)-√7x+3=0
5*|x|-10-√7x+3=0
-√7x+3=-5*|x|+10
√7x+3=5*|x|-10
7x+3=25*|x|²-100*|x|+100
7x+3=25x²-100*|x|+100
7x-25x²+100*|x|=100-3
7x-25x²+100*|x|=97
7x-25x²+100x=97, x рівне більше 0
7x-25x²+100*(-x)=97, x < 0
x=107+√1749/50
x=107-√1749/50
0=2,87183
0=0
x≠107-√1749/50
x=107+√1749/50
x≈2,97642
По графіку:
Область визначення x€(-3/7;2) (2;+безкінечність)
Перетин з віссю ординат (0; 5√3/3+1/2)