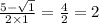Question

A)x^2+6x+8
б)x^2-8x+15
в)x^2+3x+2
г решить

Answer 1

Объяснение:

a)x²+6x+8

Д=6²–4*1*8=36–32=4

х(1)=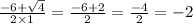 $\frac{ - 6 + \sqrt{4} }{2 \times 1} = \frac{ - 6 + 2}{2} = \frac{ - 4}{2} = - 2$

х(2)=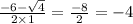 $\frac{ - 6 - \sqrt{4} }{2 \times 1} = \frac{ - 8}{2} = - 4$

б)x²-8x+15

Д=(–8)²–4*1*15=64–60=4

х(1)=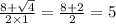 $\frac{8 + \sqrt{4} }{2 \times 1} = \frac{8 + 2}{2} = 5$

х(2)=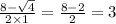 $\frac{8 - \sqrt{4} }{2 \times 1} = \frac{8 - 2}{2} = 3$

в)x²+3x+2

Д=3²–4*1*2=9–8=1

х(1)=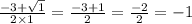 $\frac{ - 3 + \sqrt{1} }{2 \times 1} = \frac{ - 3 + 1}{2} = \frac{ - 2}{2} = - 1$

х(2)=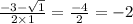 $\frac{ - 3 - \sqrt{1} }{2 \times 1} = \frac{ - 4}{2} = - 2$

г)x²-5x+6

Д=(–5)²–4*1*6=25–24=1

х(1)=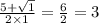 $\frac{ 5 + \sqrt{1} }{2 \times 1} = \frac{6}{2} = 3$

х(2)= $\frac{5 - \sqrt{1} }{2 \times 1} = \frac{4}{2} = 2$