Постройте график квадратичной функции и опишите её свойства у=-2х²+8х-6
Объяснение:
у=-2х²+8х-6 ,это парабола ,ветви вниз ( -2<0).
1) Координаты вершины :
х₀=-в/2а, х₀=-8/(-2*2)=2 , у₀=-2*4+8*2-6=2, (2; 2).
2)Точки пересечения с осью ох ( у=0) ;
-2х²+8х-6 =0 , х²-4х-+3=0 , х₁=1 , х₂3 . Тогда ( 1;0) , (3;0).
3) Точки пересечения с осью оу(х=0);
у(0)=-2*0²+8*0-6 =-6 , Тогда ( 0; -6).
4) Доп.точки у=-2х²+8х-6 :
х: -1 4
у: -16 -6
Свойства функции у=-2х²+8х-6 :
а) Возрастает при х∈(-∞ ;2}, убывает при х∈[2 ;+∞).
б) Принимает положительные значения ( у>0) при х∈(1 ; 3) .
Принимает отрицательные значения (y<0) при х∈(-∞ ;1)∪(3 ;+∞).
Принимает значения равные нулю ( у=0) при х=1, 3.
в) Принимает наибольшее значение у=2 при х=2.
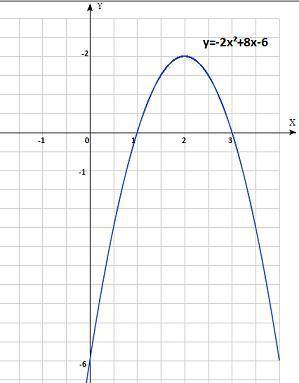
График во вложении
х - это аргумент
у - это значение функции
1. у=-1, при х=2
2. х=2, при у=-1
Проверка: 1. y=-2*2+3 => y=-4+3 => y=-1
2. -1=-2x+3 => x=(-1-3)/-2 => x=-4/-2 => x=2