Объяснение: это первый шаг теперь второй теперь из первого уравнения xy=1 подставим во второе 3*1+2y²=1 => y²=-1 что не может быть остальные случаи я тоже рассмотрел там выходит тоже самое а значит нет решений ; 4) здесь же можно сразу собрать в формулу рассмотрим вторую систему и случаи при которых равенство верное их всего 2 а остальные два не подходят тогда в первом 1) x-y-2=1 x-y=3 подходит так как x-y=3 ; x-y=3 2) x-y-2=-3 x-y=-1 что тоже подходит теперь их нужно проверить подставим в первую систему x-y=3 => x=y+3 мы получим тогда первое решение (-1;-4) второе (6;3) теперь рассмотрим второй случай когда x=y+1 подставим и решим получим третье решение (5;4) и четвертое (-2;-3) пятое задание на фото
Первым шагом будет найти производную функции s(t), чтобы найти скорость тела. Используя правило дифференцирования суммы и правило дифференцирования синуса, получим:
s'(t) = 1 + 2cos(2t)
Теперь мы можем найти скорость тела в момент времени t = 3π/4, подставив этот момент времени в выражение для производной:
Объяснение: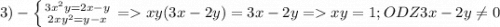
это первый шаг теперь второй 
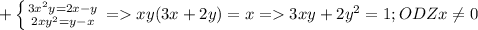теперь из первого уравнения xy=1 подставим во второе 3*1+2y²=1 => y²=-1 что не может быть остальные случаи я тоже рассмотрел там выходит тоже самое а значит нет решений ; 4) здесь же можно сразу собрать в формулу 
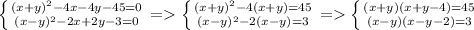рассмотрим вторую систему и случаи при которых равенство верное их всего 2 а остальные два не подходят тогда в первом 1) x-y-2=1 x-y=3 подходит так как x-y=3 ; x-y=3 2) x-y-2=-3 x-y=-1 что тоже подходит теперь их нужно проверить подставим в первую систему x-y=3 => x=y+3 мы получим 
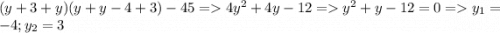тогда первое решение (-1;-4) второе (6;3) теперь рассмотрим второй случай когда x=y+1 подставим и решим 
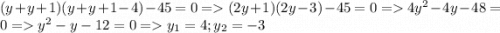получим третье решение (5;4) и четвертое (-2;-3) пятое задание на фото