x−y=x+(−y), т.к. x-y=x-y
x⋅(−y)=−xy,; т.к. -xy=-xy
(−x):(−y)=x:y, т.к.x:y=x:y
x−(−y)=x+y, т.к. x+y=x+y
все, кроме последнего.
Р пр-ка = 60 м
Sдор. = 64 м²
шир. дор. = ? м
Решение.
Если а и b - длина и ширина, соответственно, м, то
Рпр-ка = 2а + 2b ---- периметр здания
х, м ---- ширина дорожки
Площадь дорожки складывается из 8 участков, Двух равных по длине длине здания, двух равных по длине ширине здания и четырех квадратов по углам, со стороной равной стороне дорожки.
Sдор. = 4х² + 2ах + 2bх = 4х² + х(2а + 2b) = 4х² + х*Рпр-ка
4х² + 60х = 64 ----- по условию | : 4
х² + 15х - 16 = 0
D = 15² + 4*16 = 225 + 64 = 289 = 17²
х₁ =(-15 + √17²)/2 = (-15+17)/2 = 1 (м) ----- ширина дорожки
х₂ = (-15 - 17)/2 = - 16 м -- отбрасываем, как посторонний корень, не имеющий физического смысла
ответ: 1 м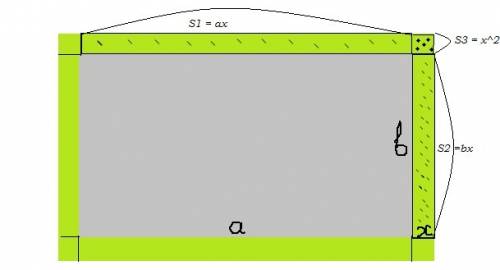
Объяснение:
1. Решением уравнения -5х-3у- 1 = 0 являются пары чисел:
А) (-1;2)
Б) (1,5;0)
В) (1;-2) -5*1+6-1=0
С) (-3;5)
2. График уравнения 4х+2у-3 = 0 пересекает ось абсцисс в точке:
А )(0; 0)
Б)(0,5; 0)
В)(0;- 0,2)
С)(0,75; 0) у=0 4х+0=3 4х=3 х=3/4=0,75
3. Из уравнения 2х-3у+4 =0 переменная у выражается через х формулой :
А ) у = (-4 – 2х)/3
Б )у = (4 – 2х)/3
В )у = (4 + 2х)/(-3)
С)у = (4 + 2х)/3 -3у=-4-2х 3у=4+2х у=(4+2х)/3
4. График уравнения у -9 = 0 на координатной плоскости расположен:
у=9
А) параллельно оси у и проходит через точку х = 9
Б) параллельно оси у и проходит через точку х = -9
В) параллельно оси х и проходит через точку у = 9
С) параллельно оси х и проходит через точку у = -9
5.
Изобразите схематично график уравнения, если известно, что это прямая, пересекающая ось у над осью х, и пересекающая ось х слева от оси у. Уравнение этой прямой:
А) 7х - 2у + 10 = 0
Б) 7х + 2у - 10 = 0
В) -7х - 2у + 10 = 0
С) -7х + 2у - 10 = 0
6
Известно, что пара чисел (-2; 2) является решением уравнения 5х + ву - 4 = 0. Найдите в.
Подставить в уравнение известные значения х и у и вычислить в:
5*(-2)+в*2-4=0
-10+2в=4
2в=4+10
2в=14
в=7
x−y=x+(−y); x-y=x-y
x⋅(−y)=−xy ; -xy=-xy
(−x):(−y)=x:y ; x:y=x:y
x−(−y)=x+y; x+y=x+y
Тождества