

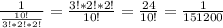
Объяснение:
Самым легким построения любой функции является построение функции поточечно.
Для первой функции y=||x|-6| подставляем вместо x точки 0,+-1,+-2,+-3 и т.д., и тем самым находим соответствующие y.
Аналогично для второй функции.
Если же требуется обосновать свое решение, то решение следующее. Модуль означает, что все отрицательные значение следует отобразить зеркально из нижней полуплоскости(3 и 4 четвертях) в верхнюю полуплоскость(1 и 2 четверти). В случае первой функции |x| будет означать то, что для левой верхней части (2 четверти), значения функции будут точно такими же, что справа сверху(1 четверть).
Привожу графики в фотографиях.


Рассмотрим x2+bx+c. Найдем пару целых чисел, произведение которых равно c, а сумма равна b. В данном случае произведение равно 34, а сумма равна −19.
−17,−2
Запишем разложение на множители, используя эти целые числа.(x−17)(x−2)
Короче:
D=b²-4ac=19×19-4×1×34=361-136=225
X1/2=-b±D/2a= -19±15/2×1=-2;-17.
ответ: (x−17)(x−2)
Вроде так)