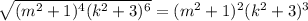Получается
здесь не надо 2 неизвестных. Среднее арифметическое пяти чисел получили путем деления суммы всех 5- чисел на 5; Значит, чтобы узнать сумму этих 5 чисел, надо среднеарифметическое значение умножить на 5; А так, как к сумме 5 чисел добавили ещё 6 число Х, то сумма шести чисел будет равна [ (-3,2) * 5 + Х ]
А среднее арифметическое значение этих 6-ти чисел равно 1. [ (-3,2) * 5 + Х ] / 6 = 2,4; и 2) [ (-3,2) * 5 + Х ] / 6 = 8 2/3; Из этих простых уравнений находим Х. Ангелина права, ответ в первом случае :30,4.
Получается
здесь не надо 2 неизвестных. Среднее арифметическое пяти чисел получили путем деления суммы всех 5- чисел на 5; Значит, чтобы узнать сумму этих 5 чисел, надо среднеарифметическое значение умножить на 5; А так, как к сумме 5 чисел добавили ещё 6 число Х, то сумма шести чисел будет равна [ (-3,2) * 5 + Х ]
А среднее арифметическое значение этих 6-ти чисел равно 1. [ (-3,2) * 5 + Х ] / 6 = 2,4; и 2) [ (-3,2) * 5 + Х ] / 6 = 8 2/3; Из этих простых уравнений находим Х. Ангелина права, ответ в первом случае :30,4.
1)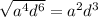
2)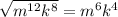
3)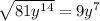
4)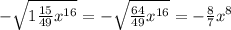
5)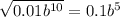
6)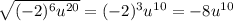
7)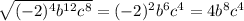
8)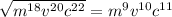
9)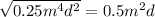
10)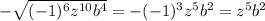
11)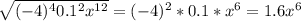
12)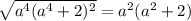
13)