1. Используя формулу n-го члена арифметической прогрессии: an = a1 + (n-1)d, решим следующую систему уравнений
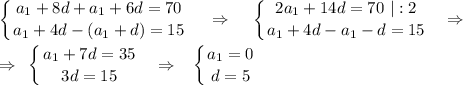
***************************************************************************************************
2. 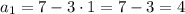
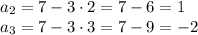
Имеем арифметическую прогрессию с первым членом 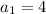 и разностью прогрессии
и разностью прогрессии 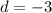
Сумма первых 12 членов арифметической прогрессии, равна:
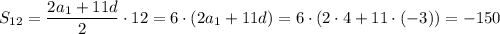
**************************************************************************************************
3. Разность прогрессии: 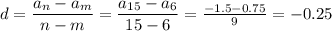
Первый член арифметической прогрессии: 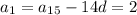
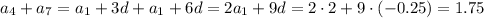
Объяснение:
1)y'=3x^2+6x, x''=6x+6, y'''=6
2)y'=2e^2x, y''=4e^2x, y'''=8e^2x,
3)y'=-sinx*e^cosx, y''=(-sinx)'*e^cosx-sinx*(e^cosx)'=
-cosx*e^cosx-sinx*(-sinx)*e^cosx=e^cosx(sin^2x-cosx)
4)y'=1/(1+x^2), y''=-2x/(1+x^2)^2