Поставим перед собой задачу: пусть нам надо решить целое рациональное неравенство с одной переменной x вида r(x)<s(x) (знак неравенства, естественно, может быть иным ≤, >, ≥), где r(x) и s(x) – некоторые целые рациональные выражения. Для ее решения будем использовать равносильные преобразования неравенства.
Перенесем выражение из правой части в левую, что нас приведет к равносильному неравенству вида r(x)−s(x)<0 (≤, >, ≥) с нулем справа. Очевидно, что выражениеr(x)−s(x), образовавшееся в левой части, тоже целое, а известно, что можно любоецелое выражение преобразовать в многочлен. Преобразовав выражение r(x)−s(x) в тождественно равный ему многочлен h(x) (здесь заметим, что выражения r(x)−s(x) иh(x) имеют одинаковую область допустимых значений переменной x), мы перейдем к равносильному неравенству h(x)<0 (≤, >, ≥).
В простейших случаях проделанных преобразований будет достаточно, чтобы получить искомое решение, так как они приведут нас от исходного целого рационального неравенства к неравенству, которое мы умеем решать, например, к линейному или квадратному. Рассмотрим примеры.
1)
У=-2х^2+5х+3
-4 =-2х^2+5х+3
-2х^2+5х+7 = 0
D = 25+ 2*7*4 = 25+56 = 81
корень из D = 9
х1 = (-5 +9)/(-4) = -1
х2 = (-5 -9)/(-4) = 3,5
2) (файл прикреплю)
а) y=9/4+3-8=5.25-8= -2.75
б) x^2-2x-11=0
x1=1+2√3
x2=1-2√3;
3) (от -∞ до -2] и [от 4 до +∞)
4) (от -∞ до 1]
3)
ибо ветви направлены вниз, то вершина параболы принимает наибольшее значение.
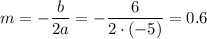
тогда, подставив х=0,6 в заданную функцию, получаем наибольшее значение функции:
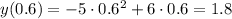
Наименьшего значения функции нет.
как то так наверное....
https://ru-static.z-dn.net/files/d0c/b840827e4223ecccede8572e809f0887.jpg
2(y-8)*(3x-4) это ответ