1) Знак неравенства меняется если основное число меньше 1;
2) Если знак неравенства, то точка будет неполная;
3) Если знак неравенства больше равно, меньше равно, то точка будет полная.
4) Полная точка ( зарисованная внутри );
5) Неполная точка ( не зарисованная внутри );
6) Если знак неравенства, то скобка "(" ;
7) Если знак неравенства больше равно, меньше равно, то скобка
"[" ;
8) В какую сторону показывает носик неравенства, в ту сторону рисуем допустимые значения;
9) Не забываем что числа можно подавать как меньшее число в степени;
Теперь когда всё вспомнили можно решать:
1) 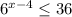
Подаём число 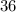 как
как 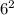
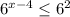
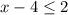
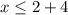
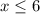
Не забываем что можно сократить основы если они одинаковые.
Теперь рисуем прямую и на ней отмечаем точку которую получили.
Фото прямых прикрепил.
Точка полная так как имеем 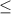 .
.
Допустимые значения направленные в левую сторону так как "носик" знака неравенства направлен именно туда.
x ∈ ( -∞, 6 ]
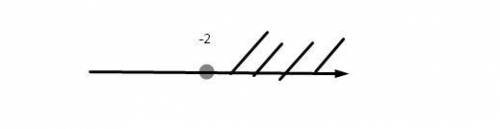
2) 
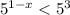
Подаём число 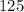 как
как 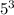
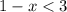
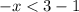
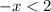
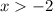
Сменили знак неравенства, так как перенесли - в другую часть неравенства.
Теперь рисуем прямую и на ней отмечаем точку которую получили.
Точка неполная, так как имеем > .
x ∈ ( -2, +∞ )
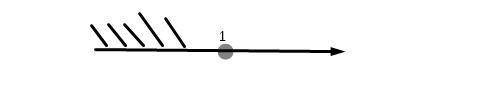
3) 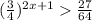
Подаём 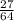 как
как 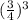 .
.
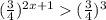
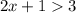
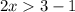
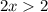
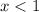
Сменили знак неравенства, так как 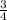 меньше 1.
меньше 1.
Теперь рисуем прямую и на ней отмечаем точку которую получили.
Точка неполная, так как имеем  .
.
x ∈ ( -∞, 1 )

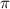 k, k ЄZ
k, k ЄZ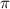 k, k ЄZ
k, k ЄZ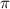 k, kЄZ
k, kЄZ 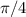 +
+ 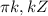
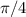 +
+ 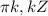
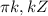
z∈(-∞; -4]∪[4;+∞)
Объяснение:
Выражение под корнем должно быть неотрицательным. Это достигается, когда оба множителя либо неотрицательны, либо оба множителя одновременно отрицательны. Решение смотри в приложении. Нулями функции f(z)=(z-4)(z+4) будут (-4) и 4. Если отметить их на прямой и рассмотреть три промежутка, то можно найти промежутки, где функция положительна и промежутки, где функция отрицательна.