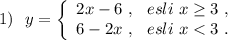
График кусочно-линейной функции состоит из нескольких частей (кусочков). Функция задаётся разными аналитическими выражениями на различных промежутках. Вне указанных промежутков линии либо стираются, либо рисуются штриховыми линиями .
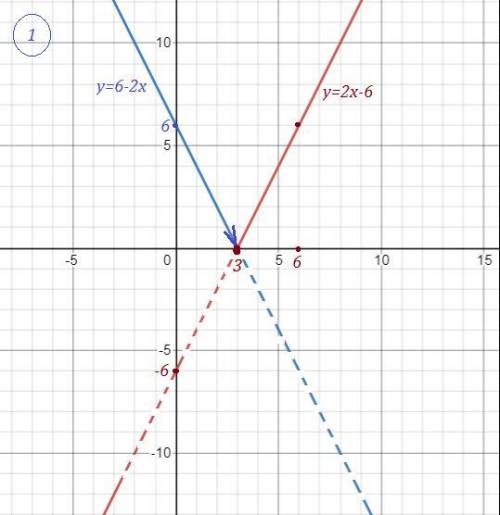
На промежутке 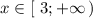 рисуем прямую у=2х-6. Она проходит через точки (3;0) и (6;6) . Вне этого промежутка линия нарисована штрихом, но её можно и стереть. Точка (3;0) принадлежит этой прямой, так как х=3 входит в указанный промежуток.
рисуем прямую у=2х-6. Она проходит через точки (3;0) и (6;6) . Вне этого промежутка линия нарисована штрихом, но её можно и стереть. Точка (3;0) принадлежит этой прямой, так как х=3 входит в указанный промежуток.
На интервале 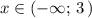 рисуем прямую у=6-2х . Она проходит через точки (3;0) и (0;6) . Вне этого промежутка линия нарисована штрихом, но её можно и стереть. Точка (3:0) не принадлежит этой прямой.
рисуем прямую у=6-2х . Она проходит через точки (3;0) и (0;6) . Вне этого промежутка линия нарисована штрихом, но её можно и стереть. Точка (3:0) не принадлежит этой прямой.
График нарисован сплошными линиями .
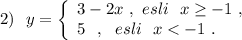
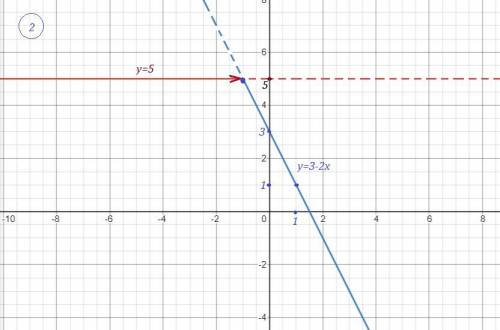
Строим прямую у=3-2х , проходящую через точки (-1;5) и (1;1) , на промежутке 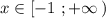 . Точка (-1;6) принадлежит графику .
. Точка (-1;6) принадлежит графику .
Прямая у=5 - это прямая, параллельная оси ОХ, проходящая через точку (0;5) . Строим её на интервале 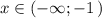 . Точка (-1;5) не принадлежит графику .
. Точка (-1;5) не принадлежит графику .
График нарисован сплошными линиями .
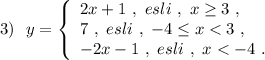
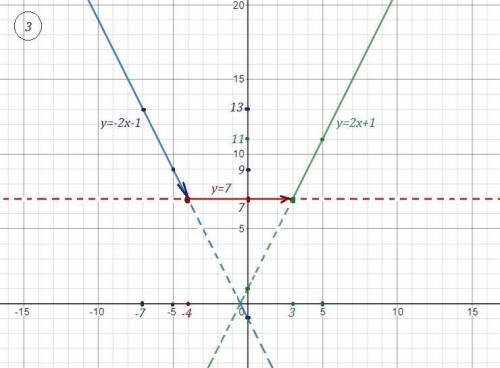
Строим прямую у=2х+1 , проходящую через точки (3;7) и (5;11) , на промежутке 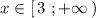 . Точка (3;7) принадлежит графику .
. Точка (3;7) принадлежит графику .
Прямая у=7 - это прямая, параллельная оси ОХ, проходящая через точку (0;7) . Строим её на промежутке 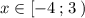 . Точка (-4;7) принадлежит графику , а точка (3;7) не принадлежит графику .
. Точка (-4;7) принадлежит графику , а точка (3;7) не принадлежит графику .
Прямую у=-2х-1 , проходящую через точки (-4;7) и (-7;13) , строим на промежутке ![x\in (-\infty ;\, -4\ ]](/tpl/images/1797/7262/3887f.png) . Точка (-4;7) не принадлежит графику .
. Точка (-4;7) не принадлежит графику .
График нарисован сплошными линиями .
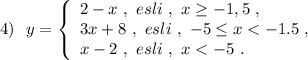
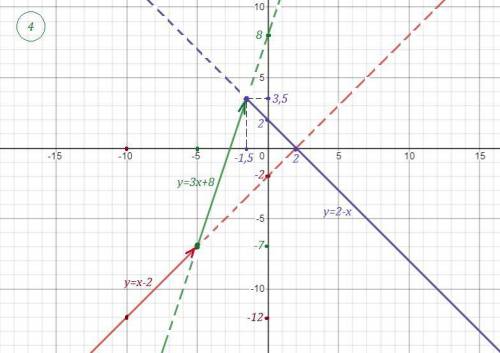
Прямую у=2-х , проходящую через точки (-1,5; 3,5) и (2;0) , строим на промежутке 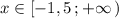 . Точка (-1,5; 3,5) принадлежит графику .
. Точка (-1,5; 3,5) принадлежит графику .
Прямую у=3х+8 , проходящую через точки (-1,5; 3,5) и (-5;-7) , строим на промежутке 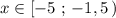 . Точка (-1,5; 3,5) не принадлежит графику .
. Точка (-1,5; 3,5) не принадлежит графику .
Прямую у=х-2 , проходящую через точки (-5; -7) и (-10;-12) , строим на промежутке 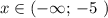 . Точка (-5; -7) не принадлежит графику .
. Точка (-5; -7) не принадлежит графику .
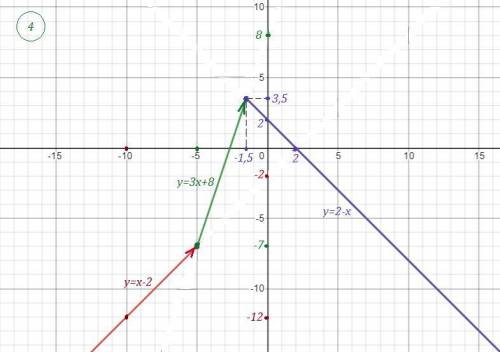
График нарисован сплошными линиями . На последнем рисунке нарисован заданный график без штриховых линий.
Объяснение:
1) а) (x-1)(x-3)>0
Допустим (x-1)(x-3)=0
x-1=0; x₁=1
x-3=0; x₂=3
Возьмём пробную точку на промежутке (-∞; 1) для определения знака функции, например, 0:
(0-1)(0-3)=-1·(-3)=3; 3>0
+ - +
°°>x
1 3
ответ: x∈(-∞; 1)∪(3; +∞).
б) (x+2)(x-5)<0
Допустим (x+2)(x-5)=0
x+2=0; x₁=-2
x-5=0; x₂=5
Пробная точка: 0.
(0+2)(0-5)=-2·5=-10; -10<0
- + -
°°>x
-2 5
ответ: x∈(-2; 5).
в) (x+9)(x+1)(x-11)>0
Допустим (x+9)(x+1)(x-11)=0
x+9=0; x₁=-9
x+1=0; x₂=-1
x-11=0; x₃=11
Пробная точка: 0.
(0+9)(0+1)(0-11)=9·1·(-11)=-99; -99<0
- + - +
°°°>x
-9 -1 11
ответ: x∈(-9; -1)∪(11; +∞).
г) x(x+8)(x-17)≤0
Допустим x(x+8)(x-17)=0
x₁=0
x+8=0; x₂=-8
x-17=0; x₃=17
Пробная точка: 2.
2(2+8)(2-17)=2·10·(-15)=10·(-30)=-300; -300<0
+ - + -
...>x
-8 0 17
ответ: x∈(-∞; -8]∪[0; 17].
2) а) (x+3)(x-8)(x-20)>0
Допустим (x+3)(x-8)(x-20)=0
x+3=0; x₁=-3
x-8=0; x₂=8
x-20=0; x₃=20
Пробная точка: 0.
(0+3)(0-8)(0-20)=3·(-8)·(-20)=-24·(-20)=480; 480>0
- + - +
°°°>x
-3 8 20
ответ: x∈(-3; 8)∪(20; +∞).
б) x(x+10)(x-3)≤0
Допустим x(x+10)(x-3)=0
x₁=0
x+10=0; x₂=-10
x-3=0; x₃=3
Пробная точка: 2.
2(2+10)(2-3)=2·12·(-1)=-24; -24<0
+ - + -
...>x
-10 0 3
ответ: x∈(-∞; -10]∪[0; 3].