x2=3*2^2-1/4*2^2+1=12-1/16+1=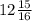
x100=3*100^2-1/4*100^2+1=30000+1-1/40000=30000\frac{39999}{40000}
последовательность является строго монотонной возрастающей, но не имеет предела, так что это доказать невозможно. Строго монотонна она потому что при неограниченном возрастании n первое слагаемое в рекурентной формуле неограниченно возрастает, а второе слагаемое постоянно убывает, в то время как 3е остается неизменным. То есть на каждом новом шаге мы все из большего вычитаем все меньшее. А предела не имеет так как послеовательноть не является ограниченной, это раз, и не выполняется критерий коши для сходимости последовательности, т.е. она не является фундаментальной, это 2
Забыл: Xn+1=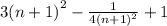
(В конце знак "/" означает дробь, не деление)
Дана система уравнений:
2x-y=8
x-3y=8
Из первого уравнения выразим х:
2x-y=8
Переносим слагаемое из левой части в правую с заменой знака:
2x=8-(-y)
2x=y+8
Делим обе части уравнения на множитель:
= 
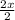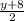
x =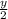 
+4
Подставляем найденное значение x во 2-ое уравнение:
x-3y=8
Получим:
-3y+(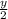+4)=8
4 - 
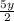=8
Переносим 4 (свободное слагаемое) из левой части в правую с заменой знака:
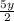-= - 4+8
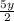-= 4
Теперь делим обе части на множитель, получается дробь (-1)5/2y /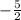 
= 4 /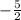
y =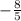 
И, т.к. x=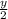+4, то x=
+4
Получается, что х =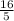 
ответ: x = 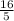, y = .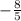
Я думаю что 12
Объясне