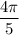Дугу можно измерять угловой мерой (размер центрального угла, опирающего на дугу) или длиной (угловая мера умноженная на радиус). Числовая окружность имеет радиус 1, поэтому значение угловой меры численно равно значению длины.
Половина окружности это π и это же длина дуги (для числовой окружности).
Наибольшое из возможных - квадрат наибольшего числа в соответствии с условием, что сумма равна 82. Тогда эти числа 41 и 41, при этом их произведение равно 1681
Пусть большее число равно х, тогда меньшее по условию равно х - 20. Их произведение равно y = x(x - 20) = x^2 - 20x. Для нахождения наименьшего возможного у берем производную от у и приравниваем нулю: y' = 2x - 20 = 0. Отсюда х = 10. Нетрудно проверить, что в этой точке у имеет минимум. Второе из чисел равно 10 - 20 = -10.
x и y y=1-x z=x(1-x) Находим критическую точку: z'=1-x-x=1-2x z'=0-> x=0,5 Проверяем какой экстремум: x<0,5->z'>0-возрастает x>0,5->z'<0-убывает, следовательно это максимум ответ:x= 0,5 и y= 0,5->xy=0,25
Дугу можно измерять угловой мерой (размер центрального угла, опирающего на дугу) или длиной (угловая мера умноженная на радиус). Числовая окружность имеет радиус 1, поэтому значение угловой меры численно равно значению длины.
Половина окружности это π и это же длина дуги (для числовой окружности).
∪AC = π = 2·∪AB ⇒ ∪AB =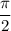
Пусть ∪AM = , тогда ∪MB =
, тогда ∪MB = 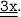
Т.к. первая четверть это ∪AB.
∪AM + ∪MB = 2x+3x = 5x =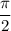 ⇒
⇒
x =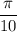 ⇒
⇒ 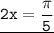 ;
; 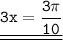
∪DM = ∪DA + ∪AM =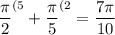
∪MC = ∪MB + ∪BC =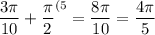
ответ: длина ∪AM =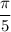
длина ∪MB =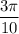
длина ∪DM =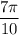
длина ∪MC =