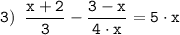
Объяснение:
Целым уравнением с одной переменной называется уравнение, левая и правая части которого - целые выражения. Отличие целого уравнения от дробно-рационального заключается в том, что областью определения целого уравнения является множество всех действительных чисел. Выполнив над целыми уравнениями равносильные преобразования можно получит уравнение вида P(x) = 0, где P(x) – многочлен в стандартном виде.
1) 3-34·(3·x-10)·(6·x+80)=7·x
3-34·(18·x²+240·x-60·x-800)=7·x
3-34·(18·x²+180·x-800)-7·x=0
3-612·x²-6120·x+27200-7·x=0
612·x²+6127·x-27203=0
P₂(x)=612·x²+6127·x-27203.
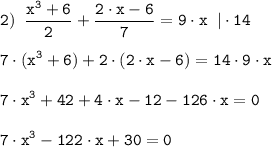
P₃(x)=7·x³-122·x+30
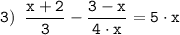
Так как в знаменателе присутствует неизвестная x, то x≠0, то есть областью определения целого уравнения не является множество всех действительных чисел.
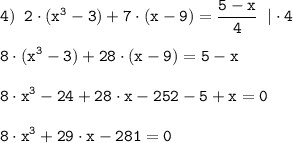
P₃(x)=8·x³+29·x-281.
Решите через систему √2x-x² +1 ≥ 2x - 3 .
√( 2x- x² +1) ≥ 2x - 3 .
ОДЗ данного неравенства: 2x - x² +1 ≥ 0 ⇔ x² - 2x - 1 ≤ 0 ⇔
x ∈ [ 1 - √2 ; 1 + √2 ] .
Будем рассматривать только эти x, другие x не могут являться решениями данного неравенства.
1.
Если 2x - 3 < 0 ,то есть x < 1,5 , то все такие x из ОДЗ , удовлетворяющие этому условию, являются решениями неравенства. Значит, все x ∈ [ 1 -√2 ; 1,5 ) − решения неравенства .
2.
Если 2x-3 ≥ 0 , то есть x ≥ 1,5 ,а с учетом ОДЗ это означает, что 1,5≤ x ≤ 1 + √2 , иначе x ∈ [ 1,5 ; 1+√2] ,то обе части неравенства неотрицательны.
Возведём обе части неравенства в квадрат:
2x- x² +1 ≥ ( 2x - 3 )² ;
2x- x² +1 ≥ 4x² - 12x +9 ;
5x² -14x +8 ≤ 0 ;
Уравнение 5x² -14x +8 =0 имеет корни x₁ =(7-3)/5 =4/5 и x₂=(7+3)/5=2
Значит, решением неравенства являются x∈ [ 0,8 ; 2].
С учётом x ∈ [ 1,5 ; 1+√2] получается, что на данном множестве решениями являются x ∈ [ 1,5 ; 2] . Объединяя результаты пунктов 1 и 2, получаем x ∈ [ 1 -√2 ; 1,5 ) ∪ [ 1,5 ; 2] , т.е. x ∈ [ 1 -√2 ; 2] .
ответ : x ∈ [ 1 -√2 ; 2] .
* * * * * * * * * * * * P.S. * * * * * * * * * * * *
Это решение можно записать другим
⇔ совокупности двух систем неравенств
[ { 2x - 3 < 0 ; 2x - x² +1 ≥ 0 .
[ { 2x - 3 ≥ 0 ; x² - 2x- 1 ≥ (2x - 3)² .