y=12⋅cos(x−π3)
Используем вид записи acos(bx−c)+d
для поиска переменных, используемых для вычисления амплитуды, периода, сдвига по фазе и вертикального сдвига.
a=12
b=1
c=π3
d=0
Найдем амплитуду |a|
.
Амплитуда: 12
Определим период при формулы 2π|b|
.
Нажмите, чтобы увидеть больше шагов...
Период: 2π
Найдем сдвиг периода при формулы cb
.
Нажмите, чтобы увидеть больше шагов...
Фазовый сдвиг: π3
Найдем вертикальное смещение d
.
Вертикальный сдвиг: 0
Перечислим свойства тригонометрической функции.
Амплитуда: 12
Период: 2π
Фазовый сдвиг: π3
(на π3
вправо)
Вертикальный сдвиг: 0
Выберем несколько точек для нанесения на график.
Нажмите, чтобы увидеть больше шагов...
xf(x)π3125π604π3−1211π607π312
Тригонометрическую функцию можно изобразить на графике, опираясь на амплитуду, период, фазовый сдвиг, вертикальный сдвиг и точки.
Амплитуда: 12
Период: 2π
Фазовый сдвиг: π3
(на π3
вправо)
Вертикальный сдвиг: 0
xf(x)π3125π604π3−1211π607π312
Объяснение:
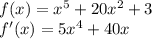
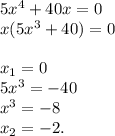
.![[-1;0]](/tpl/images/0566/4617/46aac.png)
и растёт — на промежутке ![[0;1]](/tpl/images/0566/4617/90495.png)
![f''(x)=(5x^4+40x)'=20x^3+40.\\\\20x^3+40=0\\x^3+2=0\\x^3=-2\\x= \sqrt[3]{-2}](/tpl/images/0566/4617/34390.png)
![[-1;1]](/tpl/images/0566/4617/7be0e.png)
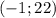является вогнутой.
и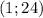 
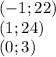
![Исследуйте функцию и постройте ее график: f(x)=x^5+20x^2+3 на промежутке [-1; 1]](/tpl/images/0566/4617/a0161.jpg)
4x+8=5x-10
4x-5x=-10-8
-x=-18
x=18
ответ:18